TdS Equations

Internally Reversible Process

A process is called internally reversible if no irreversibilities occur within the boundaries of the system during the process. During an internally reversible process, a system proceeds through a series of equilibrium states, and when the process is reversed, the system passes through exactly the same equilibrium states while returning to its initial state. That is, the paths of the forward and reverse processes coincide for an internally reversible process. The quasi-equilibrium process is an example of an internally reversible process.

For an internally reversible process, the entropy balance in a closed system equation becomes

$$\Delta S_{\text{sys}}=S_2-S_1=\sum \frac{Q_k}{T_k}+\cancel{S_{\text{gen}}}$$

since there is no entropy generation $S_{\text{gen}}$.

The above equation can be re-arranged to become

$$Q_{\text{int rev}}={\int }_1^{2}TdS$$

such that we can quantify the amount of heat transfer in the system due to change in entropy at a given temperature.

P-V : T-S Analogy - Derivation of TdS Equations

Like how moving boundary work can be expressed as $W_{1-2}={\int }_1^{2}P(V)dV$, where the area under the P-V curve is the work output, we have:

$$Q_{1-2,\text{ int rev}}={\int }_1^{2}T(s)dS$$

where the area under the Temperature-Entropy (T-S) curve is the heat input.

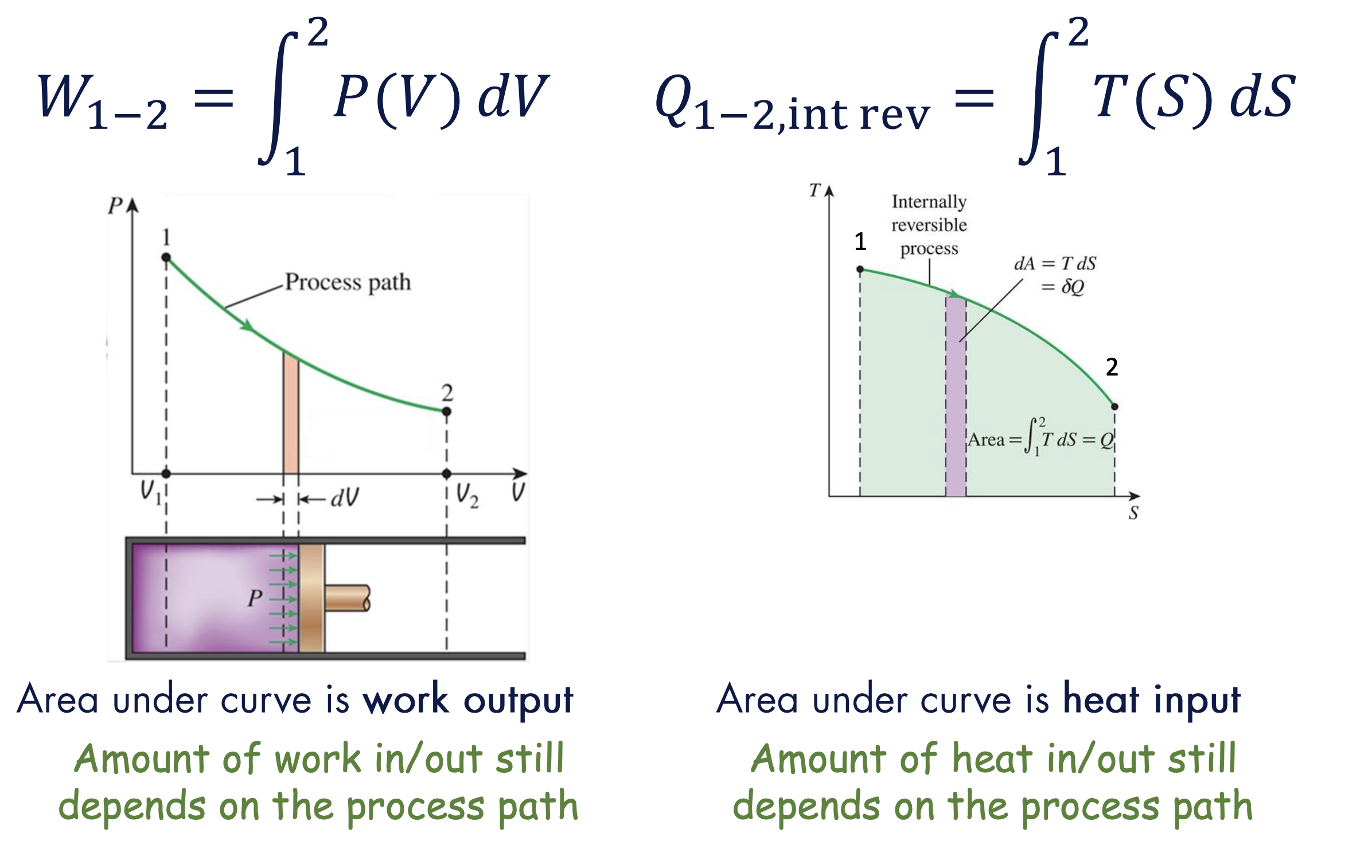
For boundary work, we can write:

$$\begin{array}{rl}{W}_{1-2}& ={\int }_1^{2}P(V)dV\\ \delta W& =PdV\end{array}$$

Similarly, for internally reversible heat transfer, we can write

$$\delta Q=TdS$$

Recall that the first law states

$$dU=\delta Q-\delta W\text{(First Law)}$$

So we have:

$$dU=TdS-PdV$$

or

$$\begin{array}{rl}TdS& =dU+PdV\text{(Extrinsic form)}\\ Tds& =du+Pdv\text{ (Intrinsic form)}\end{array}$$

This is a nice formula because $s,u,P,v$ can be found in data booklet as intensive independent properties.

The TdS Equations

Recall that we can write enthalpy as

$$h=u+Pv$$

In differential form:

$$dh=du+Pdv+vdP$$

Since we established that $Tds=du+Pdv$, we can then write:

$$\begin{array}{rl}dh& =Tds+vdP\\ Tds& =dh-vdP\end{array}$$

Thus, considering a stationary, closed system undergoing a reversible process between State 1 and State 2, we arrive at the TdS equations:

$$\boxed{\begin{array}{r}Tds=du+Pdv\\ Tds=dh-vdP\end{array}}$$

• The TdS equations relate state properties. Thus, in order to use them, equation of state must be defined, such as the P-v-T surface. See Entropy Change of Pure Substances.
• The TdS equations relate state properties, so they do not rely on the process path. They are valid for reversible or irreversible processes and closed/open systems. This is a bit of a bait and switch since we specifically used internally reversible processes to do this derivation.
• To use the TdS equations, $T$ and $P$ during the process must be known, and entropy may still be generated.

Applying TdS Equations

Recall that we apply specific heat, $c$, differently for each phase of matter to relate $\Delta u$ or $\Delta h$ to $T$.

• For solids or incompressible liquids, we can say that $c_p=c_v=c$.
• In or near the vapor dome, we use $h,u$ tabulated for $T,P$
• For ideal gases, we use $u_2-u_1={\bar{c}}_v(T_2-T_1)$ and $h_2-h_1={\bar{c}}_p(T_2-T_1)$.

Similarly, we can apply the TdS equations in convenient forms depending on the phase.

Solids + Incompressible Liquids

For solids or incompressible liquids, since the volume cannot change, we have $dv=0$. We can also write change in internal energy in terms of change in temperature as $du=cdT$. Then, our TdS equations, we have:

$$\begin{array}{rl}Tds& =du+Pdv\\ & =cdT+P(0)\\ & =cdT\end{array}$$

We can then write:

$$\begin{array}{rl}{\int }_1^{2}ds& ={\int }_1^{2}c(T)\frac{dT}{T}\\ s_2-s_1& ={\overline{c}}_{\text{avg}}\ln \left(\frac{T_2}{T_1}\right)\end{array}$$

Note that in the isentropic case, we have $s_2-s_1=0$ and $T_2-T_1=0$.

Vapor Dome

In or near the vapor dome, we use the property tables with $T,P$ to find $u,h,s$.

Ideal Gases

For ideal gases, we have $du=c_{v}dT$ and $Pv=RT$, which lets us write

$$\begin{array}{rl}Tds& =du+Pdv\\ Tds& =c_{v}dT+\left(\frac{RT}{v}\right)dv\\ \int ds& ={\int }_1^2{c}_v(T)\frac{dT}{T}+R\ln \left(\frac{v_2}{v_1}\right)\end{array}$$

This leads to

$$\begin{array}{r}{s}_2-s_1={\overline{c}}_v\ln \frac{T_2}{T_1}+R\ln \frac{v_2}{v_1}\\ s_2-s_1={\overline{c}}_p\ln \frac{T_2}{T_1}+R\ln \frac{P_2}{P_1}\end{array}$$

Example

Example 1

Example 2