With sufficient capacity, a neural network often performs perfectly on training data; however, it does not necessarily generalize well to new test data.
We will see that the test errors have three distinct causes and that their relative contributions depend on (i) the inherent uncertainty in the task, (ii) the amount of training data, and (iii) the choice of model. The latter dependency raises the issue of hyperparameter search. We discuss how to select both the model hyperparameters (e.g., the number of hidden layers and the number of hidden units in each) and the learning algorithm hyperparameters (e.g., the learning rate and batch size).
What are the sources of error that causes a model to fail to generalize?
Visual model example
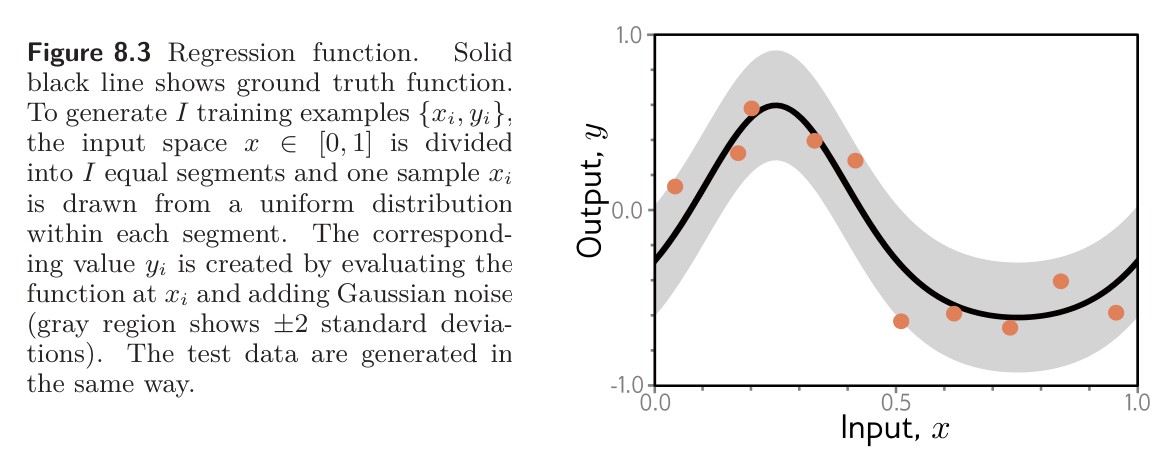
For the sake of visualization, consider 1D least squares regression problem where we know exactly how the ground truth data was generated.
Figure 8.3 shows a quasi-sinusoidal function; both training and test data are generated by sampling input values in the range , passing them through this function, and adding Gaussian noise with fixed variance.
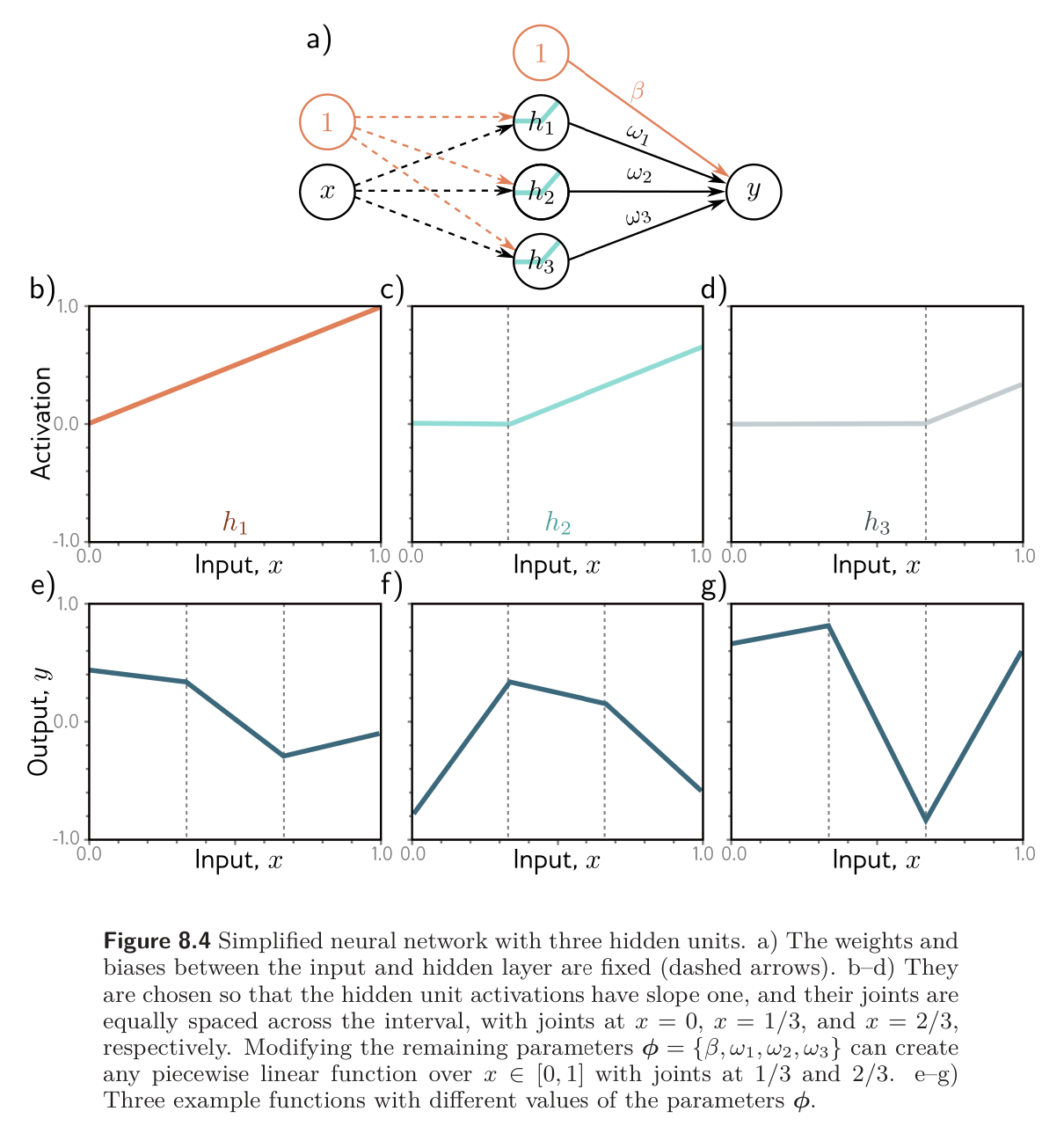
We fit a simplified shallow neural network to this data (figure 8.4). The weights and biases that connect the input layer to the hidden layer are chosen so that the “joints” of the function are evenly spaced across the interval. If there are hidden units, then these joints will be at .
This model can represent any piecewise linear function with equally sized regions in the range . As well as being easy to understand, this model also has the advantage that it can be fit in closed form without the need for stochastic optimization algorithms (see problem 8.3). Consequently, we can guarantee a global minimum of the loss function during training.
Noise, bias and variance
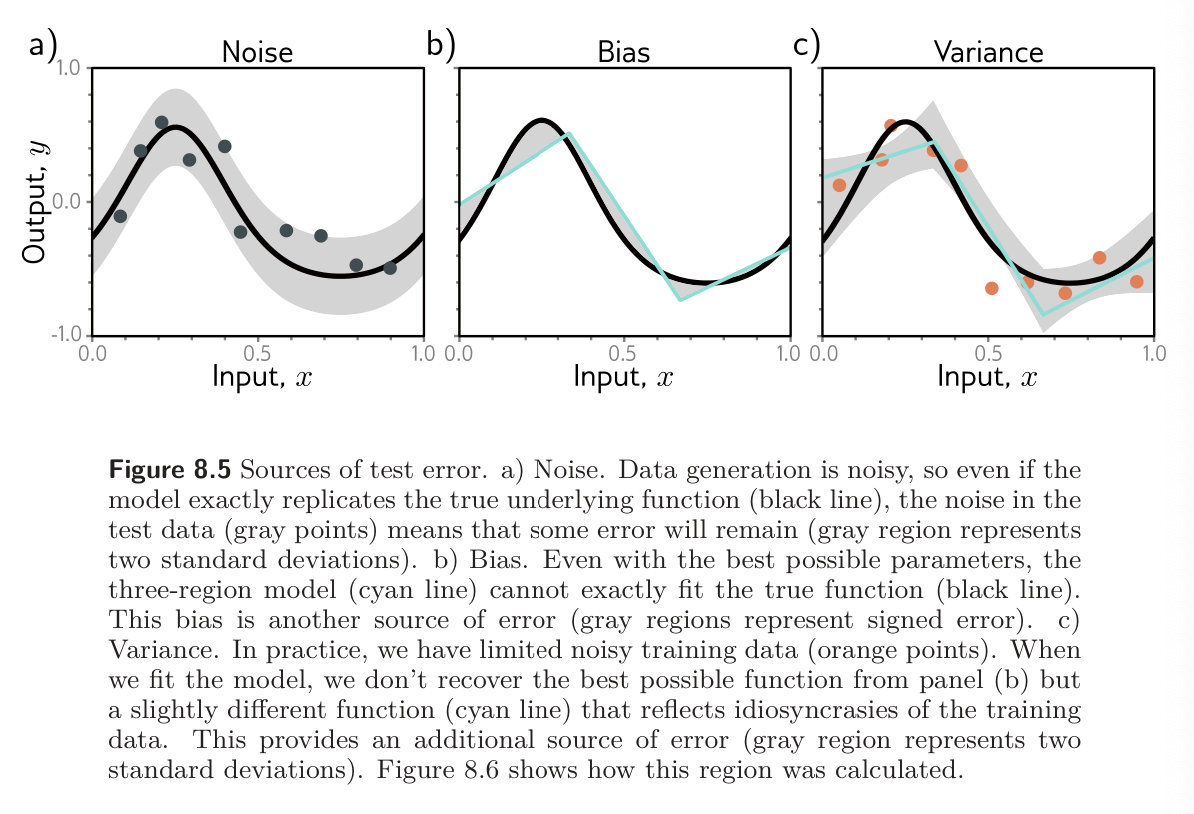
There are three possible sources of error: noise, bias, and variance. The figure below illustrates each of these for the visual model example above where we try to fit a quasi-sinusoidal function using a 3-region shallow neural network.
Noise
The data generation process includes the addition of noise, so there are multiple possible valid outputs for each input . This source of error is insurmountable for test data. It does not necessarily limit the training performance; we will likely never see the same input twice during training, so it is still possible to fit the training data perfectly.
Noise may arise because there is a genuine stochastic element to the data generation process, because some of the data are mislabeled, or because there are further explanatory variables that are not not observed. In rare cases, noise may be absent; for example, a network might approximate a function that is deterministic but requires significant computation to evaluate. However, noise is usually fundamental limitation on the possible test performance.
Bias
A second potential source of error may occur because the model is not flexible enough (lacks capacity) to fit the true function perfectly. For example, the three-region neural network cannot exactly describe a quasi-sinusoidal function, even when the parameters are chosen optimally. This is known as bias.
Variance
We have limited training samples, and there is no way to distinguish systematic changes in the underlying function from noise in the underlying data. When we fit a model, we do not get the closest possible approximation to the true underlying function. For different training datasets, the result will be slightly different each time. This additional source of variability in the fitted function is called variance. In practice, there might also be additional variance due to the stochastic learning algorithm, which does not necessarily converge to the same solution each time.