Bayes Filter

Given:

• Probabilistic Motion Model of a robot, ${\xi }_k=f({\xi }_{k-1},u_{k-1})$
• Measurement Model, $z_k=g({\xi }_k)$a

When $f(\bullet )$ and $g(\bullet )$ are corrupted by noise, ${\xi }_k$ and $z_k$ essentially become random variables and their models can be better represented by conditional probabilities:

$$\begin{array}{rl}{\xi }_k=f({\xi }_{k-1},u_{k-1})& ⟶{\xi }_k\sim p({\xi }_k|{\xi }_{k-1},u_{k-1})\\ & ⟶z_k\sim p(z_k|{\xi }_k)\end{array}$$

This is precisely the underlying spirit of the treatment of theories in probabilistic robotics.

Path, Input and Observations

For the robot state $\xi =[x,y,\theta {]}^T$, its path is defined as the sequence

$${\xi }_{0:N}=\{{\xi }_0,{\xi }_1,\dots ,{\xi }_N\}$$

Let $u$ denote the inputs (or proprioceptive sensor data), e.g. wheel encoders, velocities from IMU or motor input, etc. Then, the sequence of inputs to the robot motion is denoted by

$$u_{0:N}=\{u_0,u_1,\dots ,u_N\}$$

Let $z$ denote the exteroceptive sensors, e.g. LiDAR, GPS, vision. These are the measurements providing absolute (yet uncertain) information about the state $\xi$. Then, its sequence is

$$z_{0:N}=\{z_0,z_1,\dots ,z_N\}$$

Belief & Prediction of Robot Pose

In general, a robot cannot measure its true state (pose) directly. It only knows the best estimate of its pose based on its sensor data. Therefore, the knowledge the robot has about its state can only be inferred from data. The best guess about the robot state is called the belief.

Odometry, motion model, and all the measurement models of the sensors can be incorporated to provide us with this belief. It takes the form of a conditional probability:

$$bel({\xi }_k)=p({\xi }_k|z_{0:k},u_{0:k-1})$$

Note that the posterior $p({\xi }_k|z_{0:k},u_{0:k-1})$ represents the probability of the robot being at ${\xi }_k$ given all its past observations $z_{0:k}$ and all its past control inputs $u_{0:k-1}$.

In our localization algorithm, it’s useful to define another posterior without the most recent observation, $z_k$, i.e.:

$$\overline{bel}({\xi }_k)=p({\xi }_k|z_{0:k-1},u_{0:k-1})$$

We call $\overline{bel}({\xi }_k)$ the prediction update, meaning that the current robot pose belief is only predicted on the basis of the motion model and previous observations.

Bayes Filter

A Bayes filter is a computational procedure to obtain $bel({\xi }_k)$ recursively; we find a description of $bel({\xi }_k)$ from $bel({\xi }_{k-1})$. Different implementations of Bayes filters lead to Kalman Filter, information filter, histogram filter, particle filter.

The Bayes filter works in 2 steps for each timestep:

• Prediction: Estimate the pose using an odometry model and its numerical integration
• Correction: Refine the predicted pose using the measurements from exteroceptive sensors

Derivation

We start with:

$$bel({\xi }_k)=p({\xi }_k\mid z_{0:k},u_{0:k-1})$$

Applying Bayes rule:

$$\begin{array}{rl}bel({\xi }_k)& =\frac{p(z_k|{\xi }_k,z_{0:k-1},u_{0:k-1})p({\xi }_k|z_{0:k-1},u_{0:k-1})}{p(z_k|z_{0:k-1},u_{0:k-1})}\\ & =p({\xi }_k\mid z_{0:k},u_{0:k-1})\eta p(z_k\mid {\xi }_k,z_{0:k-1},u_{0:k-1})p({\xi }_k\mid z_{0:k-1},u_{0:k-1})\\ & =\eta p(z_k|{\xi }_k,z_{0:k-1},u_{0:k-1})p({\xi }_k|z_{0:k-1},u_{0:k-1})\end{array}$$

• $\eta$ is a normalization constant that rescales values so that $\int bel({\xi }_k)d{\xi }_k=1$

Invoking the Markov property, we note that the observation $z_k$ depend only on the current state ${\xi }_k$, not past states or old observations:

$$p(z_k\mid {\xi }_k,z_{0:k-1},u_{0:k-1})=p(z_k\mid {\xi }_k)$$

Also, recall that we defined the prediction belief:

$$\overline{bel}({\xi }_k):=p({\xi }_k\mid z_{0:k-1},u_{0:k-1})$$

Thus, we can write:

$$\begin{array}{rl}bel({\xi }_k)& =\eta \underset{=p(z_k|{\xi }_k)}{\underbrace{p(z_k|{\xi }_k,z_{0:k-1},u_{0:k-1})}}\underset{=\overline{bel}({\xi }_k)}{\underbrace{p({\xi }_k|z_{0:k-1},u_{0:k-1})}}\\ \therefore bel({\xi }_k)& =\eta p(z_k|{\xi }_k)\overline{bel}({\xi }_k)\end{array}$$

Now that we’ve written $bel({\xi }_k)$ with respect to $\overline{bel}({\xi }_k)$, let’s find a description of $\overline{bel}({\xi }_k)$ from $bel({\xi }_{k-1})$:

$$\begin{array}{rl}\overline{bel}({\xi }_k)& =p({\xi }_k|z_{0:k-1},u_{0:k-1})\\ & =\int p({\xi }_k\mid {\xi }_{k-1},z_{0:k-1},u_{0:k-1})p({\xi }_{k-1}\mid z_{0:k-1},u_{0:k-1})d{\xi }_{k-1}\end{array}$$

Invoking the Markov property or robot dynamics again, we note that the state transition only depend on the previous state and last control input:

$$p({\xi }_k\mid {\xi }_{k-1},z_{0:k-1},u_{0:k-1})=p({\xi }_k\mid {\xi }_{k-1},u_{k-1})$$

Note that $p({\xi }_{k-1}\mid z_{0:k-1},u_{0:k-1})=p({\xi }_{k-1}\mid z_{0:k-1},u_{0:k-2})$ because ${\xi }_{k-1}$ is not affected by $u_{k-1}$.

Recall that by definition, $p({\xi }_{k-1}|z_{0:k-1},u_{0:k-2})=bel({\xi }_{k-1})$:

$$\therefore \overline{bel}({\xi }_{k)}=\int p({\xi }_k\mid {\xi }_{k-1},u_{k-1})bel({\xi }_{k-1})d{\xi }_{k-1}$$

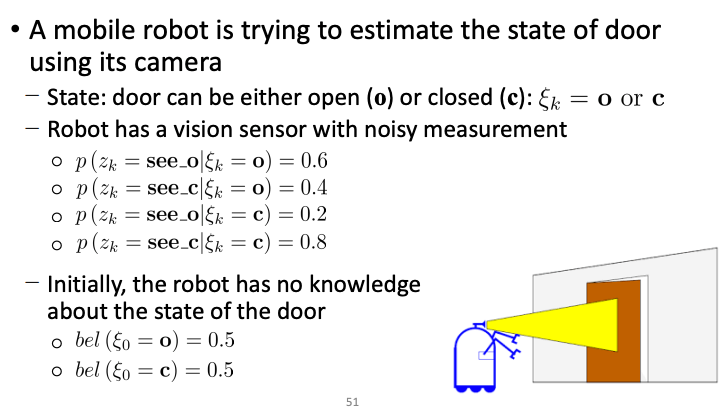
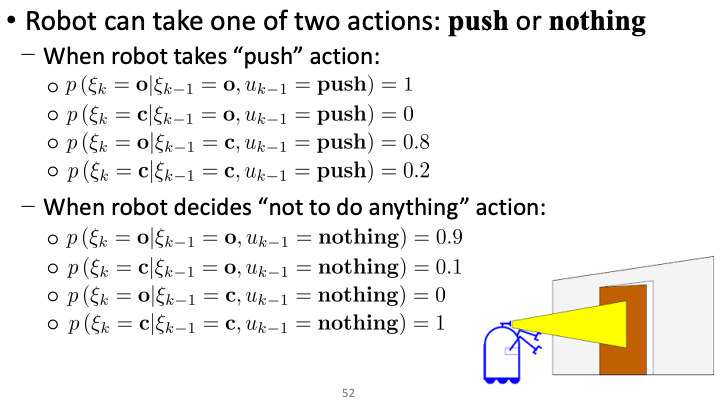
Example