Shallow vs. Deep Networks

Here we compare shallow neural networks with a single hidden layer vs deep neural networks with multiple hidden layers.

Ability to approximate different functions

We argued that shallow neural networks with enough capacity (hidden units) could model any function arbitrarily closely (Universal Approximation Theorem). We saw that a deep network with two hidden layers could represent the composition of two shallow networks (Composing Shallow Networks). If the second of these networks computes the identity function, then this deep network replicates a single shallow network. Hence, it can also approximate any continuous function arbitrarily closely given sufficient capacity.

Number of linear regions per parameter

Shallow Networks

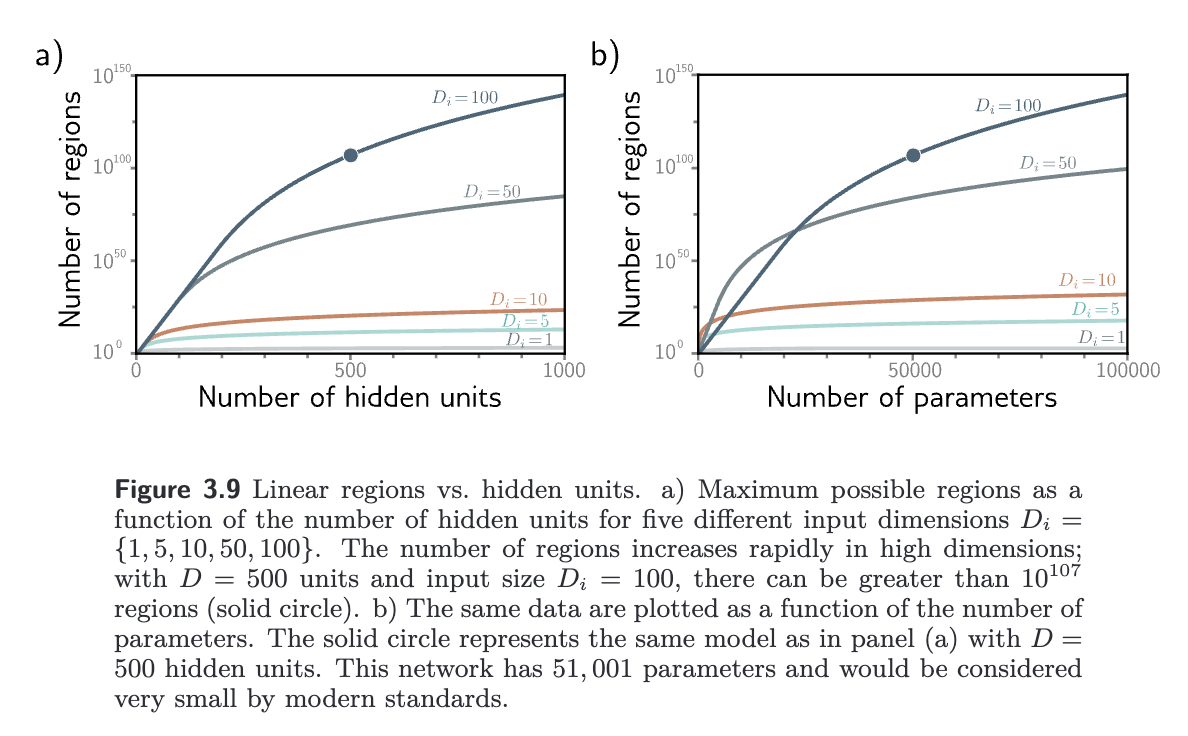
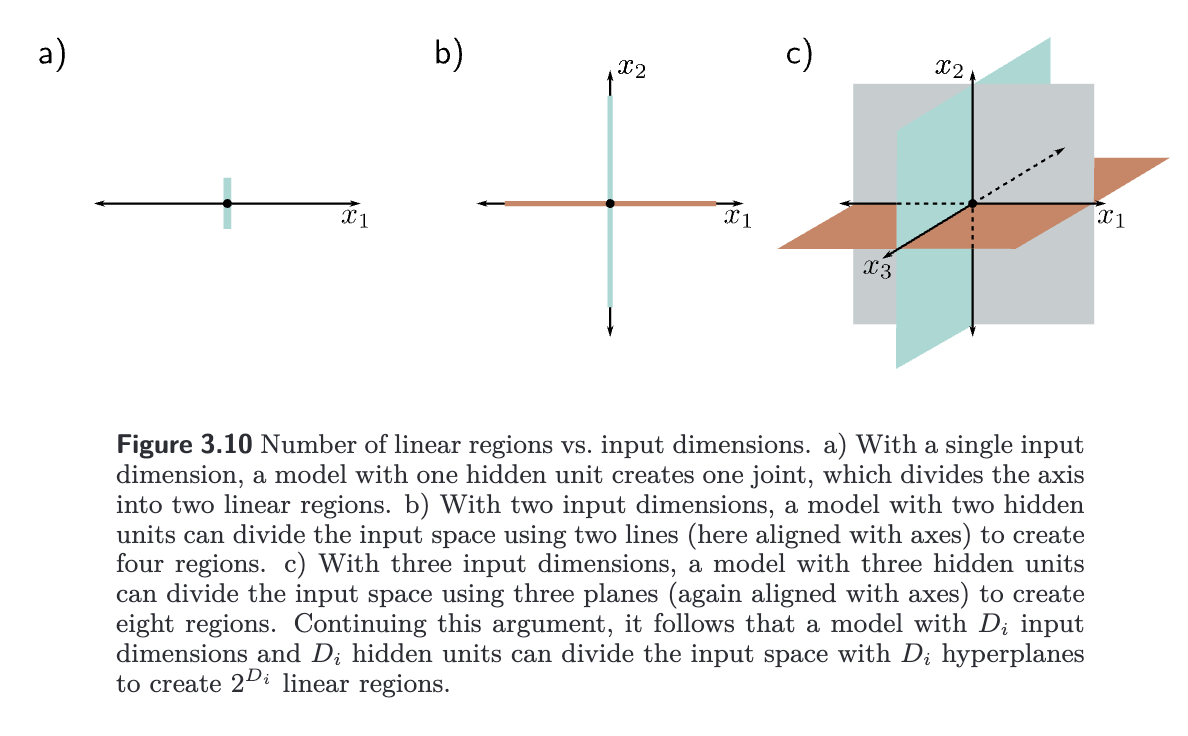
In a shallow network, as the input dimensions grow, the number of linear regions increases rapidly. Each hidden unit defines a hyperplane ($n-1$ dimensional plane) that delineates the part of the space where this unit is active from the part it is not. If we had the same number of hidden units as input dimensions $D_i$, we could align each hyperplane with one of the coordinate axes. For two input dimensions, this would divide the space into four quadrants. For three dimensions, this would create eight octants, and for $D_i$ dimensions, this would create $2^{D_i}$ orthants. hallow neural networks usually have more hidden units than input dimensions, so they typically create more than $2^{D_i}$ linear regions.

Zavslavsky’s formula: The number of regions created by $D$ hyperplanes in the $D_i\le D$-dimensional input space is at most

$$\sum _{j=0}^{D_i}\left(\genfrac{}{}{0ex}{}{D}{j}\right)$$

which is a sum of binomial coefficients.

As a rule of thumb, shallow neural networks almost always have a larger number $D$ of hidden units than input dimensions $D_i$ and create between $2D_i$ and $2D$ linear regions.

Deep Networks

• A shallow network with one input, one output, and $D>2$ hidden units can create up to $D+1$ linear regions and is defined by $3D+1$ parameters.
• A deep network with one input, one output, and $K$ layers of $D>2$ hidden units can create a function with up to $(D+1{)}^K$ linear regions using $3D+1+(K-1)D(D+1)$ parameters
  • See Problem 4.10

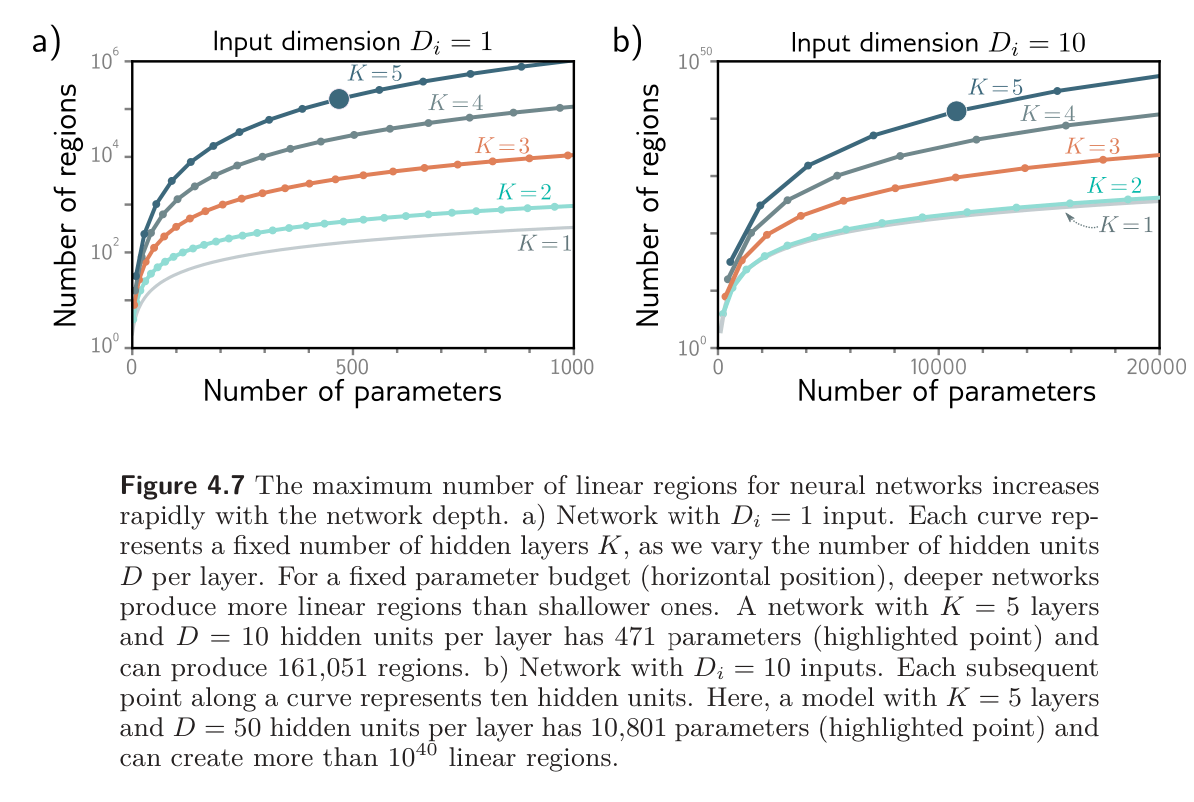
The left side of figure below shows that the number of linear regions increases as a function of the number of parameters mapping scalar input $x$ to scalar output $y$. Deep neural networks create much more complex functions for a fixed parameter budget. This effect is magnified as the number of input is magnified as the number of input $D_i$ increases (right side), although computing the maximum number of regions is less straightforward.

More linear regions seems attractive, but the flexibility of the functions is still limited by the number of parameters. Deep networks can create extremely large numbers of linear regions, but these contain complex dependencies and symmetries.

• We saw this when we thought of deep networks as composing shallow networks that fold the input space.
• It’s not clear that having more linear regions is an advantage, unless there are similar symmetries in the real-world functions that we wish to approximate, or we have reason to believe that the mapping from input to output really does involve a composition of simpler function.

Depth Efficiency

Some functions can be approximated much more efficiently with deep networks; some would require exponentially more hidden units to achieve if using a shallow network. This is referred to as the depth efficiency of neural networks. While this is theoretically attractive, it is not clear that real-world functions that we want to approximate always fall into this category.

Large, Structured Inputs

Fully connected networks, where every element of each layer contributes to every element of the subsequent one, are not practical for large, structured inputs like images, where the input might comprise $\sim 10^6$ pixels. The number of parameters would be prohibitive. We also want different parts of the image to be processed similarly; there’s no point in independently learning to recognize the same object every possible position in the image.

The solution is to process local image regions in parallel and then gradually integrate increasingly larger regions. This kind of local-to-global processing is difficult to specify without multiple layers (see Convolutional Networks).

Training & Generalization

A further possible advantage of deep networks over shallow networks is their ease of fitting; it is usually easier to train moderately deep networks than to train shallow ones. It may be that over-parameterized deep models (i.e., those with more parameters than training examples) have a large family of roughly equivalent solutions that are easy to find. However, as we add more hidden layers, training becomes more difficult again. Many methods have been developed to mitigate this problem (see chapter Residual Networks).

Deep neural networks also seem to generalize to new data better than shallow ones. In practice, the best results for most tasks have been achieved using networks with tens or hundreds of layers. Neither of these phenomena are well understood.