The derivatives of the loss tell us how the loss changes when we make a small change to the parameters. Optimization algorithms exploit this information to manipulate the parameters so that the loss becomes smaller. The backpropagation algorithm computes these parameters. We first make two observations to provide some intuition.
Observation 1: Each weight (element of ) multiplies the activation at a source hidden unit and adds the result to the destination hidden unit in the next layer. Thus, it follows that the effect of any small change to the weight is amplified or attenuated by the activation at the source hidden unit. Hence, we run the network for each data example in the batch and store the activations of all the hidden units. This is known as the forward pass. The stored activations will subsequently be used to compute the gradients.
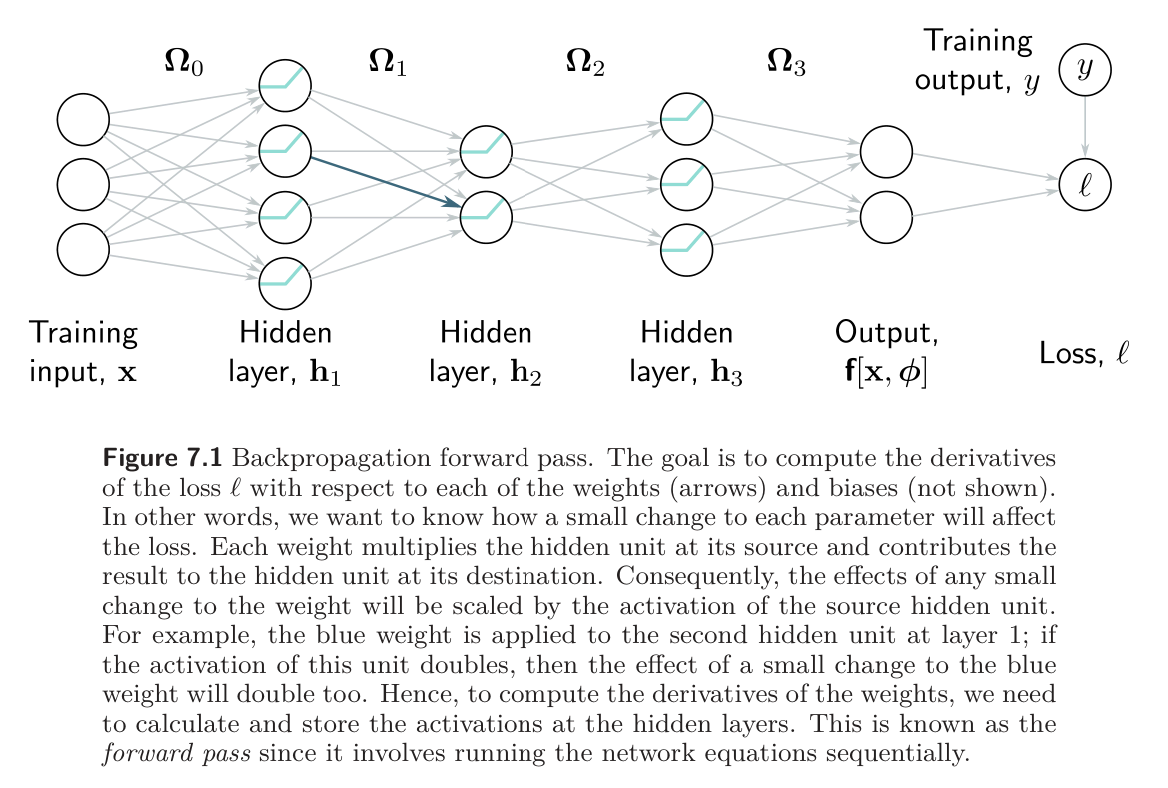
Observation 2: A small change in a bias or weight causes a ripple effect of changes through the subsequent network. The change modifies the value of its destination hidden unit. This, in turn changes the value of the hidden units in the subsequent layer, which will change the hidden units in the layer after that, and so on, until a change is made to the model output and, finally, the loss.
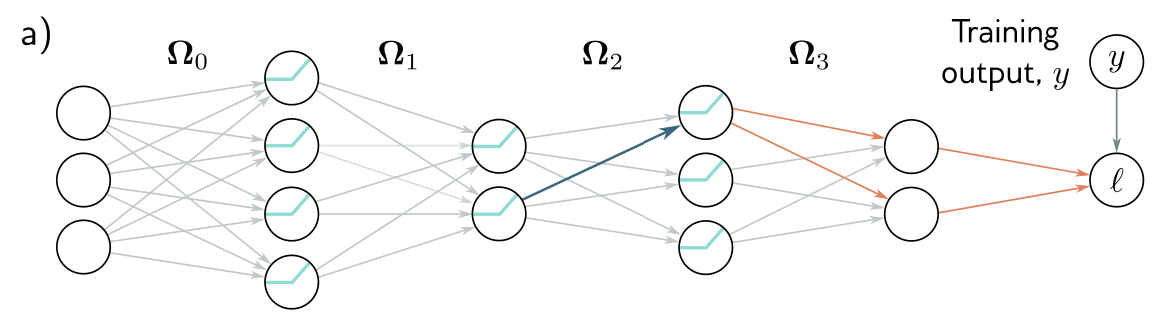
Hence, to know how changing a parameter modifies the loss, we also need to know how changes to every subsequent hidden layer will, in turn, modify their successor. These same quantities are required when considering other parameters in the same or earlier layers. It follows that we can calculate them once and reuse them. For example, consider computing the effect of a small change in weights that feed into hidden layers , , and , respectively.
To calculate how a small change in a weight or bias feeding into hidden layer modifies the loss, we need to know:
- (i) how a change in layer changes the model output
- (ii) how a change in this output changes the loss .
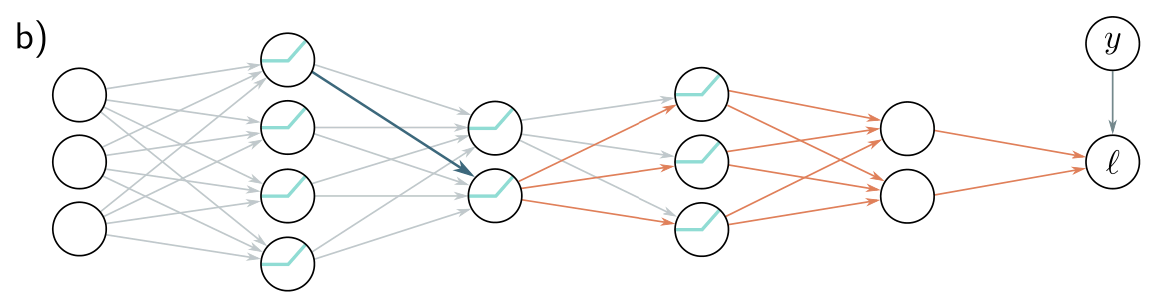
To calculate how a small change in a weight or bias feeding into hidden layer modifies the loss, we need to know:
- (i) how a change in layer affects
- (ii) how a change in layer changes the model output
- (iii) how a change in this output changes the loss .
To calculate how a small change in a weight or bias feeding into hidden layer modifies the loss, we need to know:
- (i) how a change in layer affects
- (ii) how a change in layer affects
- (iii) how a change in layer changes the model output
- (iii) how a change in this output changes the loss .
As we move backward through the network, we see that most of the terms we need were already calculated in the previous step, so we do not need to re-compute them. Proceeding backward through the network in this way to compute derivatives is known as the backward pass.