UDL Chapter 4 Problems

Problem 4.1

Consider composing the two neural networks in figure 4.8. Draw a plot of the relationship between the input $x$ and output $y^{\prime }$ for $x\in [-1,1]$.

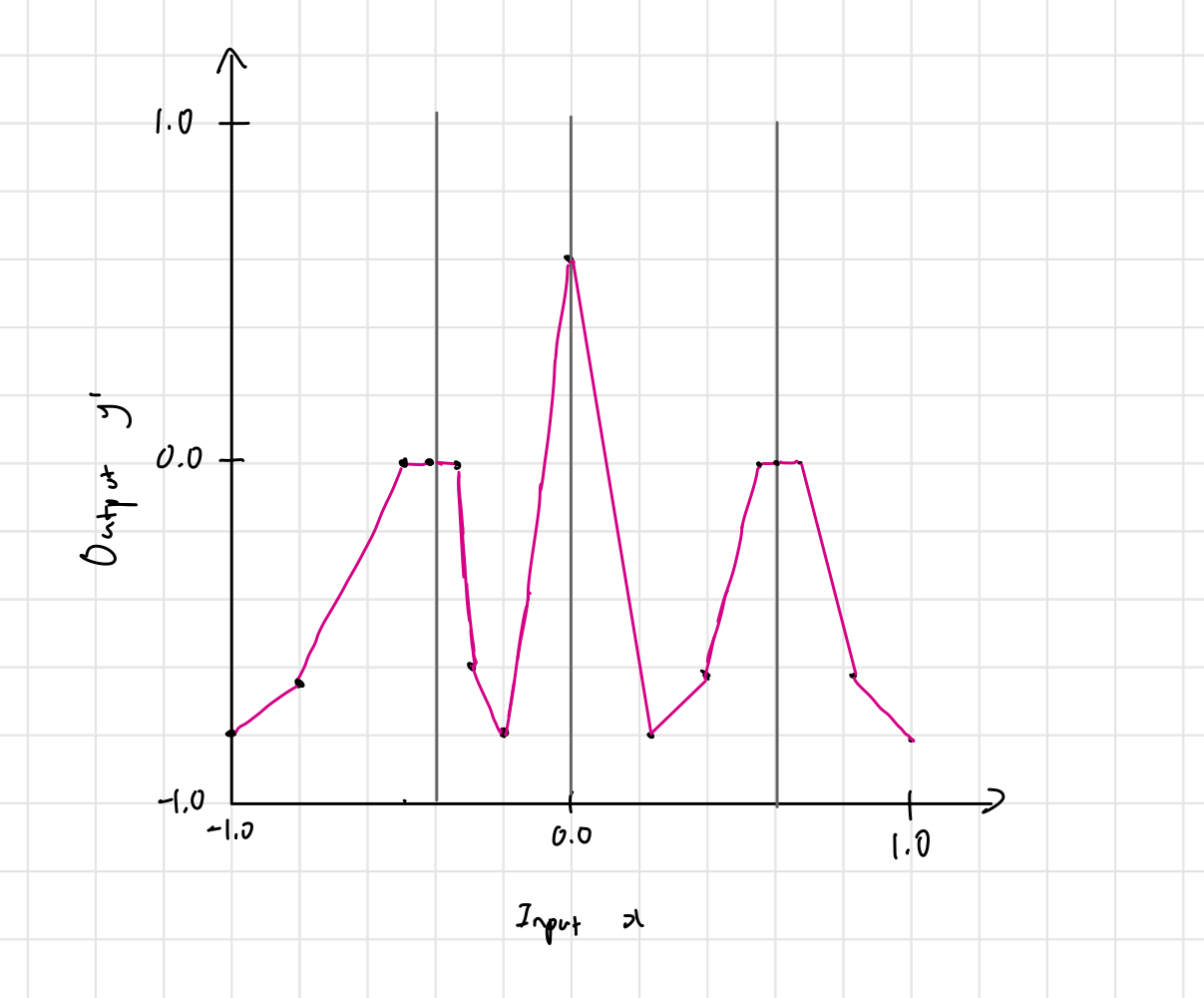
Problem 4.2

Identify the four parameters in figure 4.6.

• $K=3$
• $D_1=4$
• $D_2=2$
• $D_3=3$

Problem 4.3

Using the non-negative homogeneity property of the ReLU function (see problem 3.5), show that:

$$\text{ReLU}[{\beta }_1+{\lambda }_1\cdot {\Omega }_1\text{ReLU}[{\beta }_0+{\lambda }_0\cdot {\Omega }_0\mathbf{x}]]={\lambda }_0{\lambda }_1\cdot \text{ReLU}\left[\frac{1}{{\lambda }_0{\lambda }_1}{\beta }_1+{\Omega }_1\text{ReLU}\left[\frac{1}{{\lambda }_0}{\beta }_0+{\Omega }_0\mathbf{x}\right]\right]$$

where ${\lambda }_0$ and ${\lambda }_1$ are non-negative scalars. From this, we see that the weight matrices can be rescaled by any magnitude as long as the biases are also adjusted, and the scale factors can be re-applied at the end of the network.

The non-negative homogeneity property states that:

$$\text{ReLU}[\alpha \cdot z]=\alpha \cdot \text{ReLU}[z]$$

We have

$$\begin{array}{rl}& \text{ReLU}[{\beta }_1+{\lambda }_1\cdot {\Omega }_1\text{ReLU}[{\beta }_0+{\lambda }_0\cdot {\Omega }_0\mathbf{x}]]\\ & =\text{ReLU}\left[{\lambda }_1\cdot \left(\frac{{\beta }_1}{{\lambda }_1}+{\Omega }_1\text{ReLU}\left[{\lambda }_0\cdot \left(\frac{{\beta }_0}{{\lambda }_0}+{\Omega }_0\mathbf{x}\right)\right]\right)\right]\\ & ={\lambda }_1\text{ReLU}\left[\frac{{\beta }_1}{{\lambda }_1}+{\lambda }_0{\Omega }_1\text{ReLU}\left[\frac{{\beta }_0}{{\lambda }_0}+{\Omega }_0\mathbf{x}\right]\right]\\ & ={\lambda }_1\text{ReLU}\left[{\lambda }_0\left(\frac{{\beta }_1}{{\lambda }_1{\lambda }_0}+{\Omega }_1\text{ReLU}\left[\frac{{\beta }_0}{{\lambda }_0}+{\Omega }_0\mathbf{x}\right]\right)\right]\\ & ={\lambda }_0{\lambda }_1\text{ReLU}\left[\frac{{\beta }_1}{{\lambda }_1{\lambda }_0}+{\Omega }_1\text{ReLU}\left[\frac{{\beta }_0}{{\lambda }_0}+{\Omega }_0\mathbf{x}\right]\right]\end{array}$$

as desired.

Problem 4.4

Write out the equations for a deep neural network that takes $D_i=5$ inputs, $D_o=4$ outputs and has three hidden layers of sizes $D_1=20$, $D_2=10$, and $D_3=7$, respectively, in both the forms of equations 4.15 and 4.16. What are the sizes of each weight matrix ${\Omega }_{\bullet }$ and bias vector ${\beta }_{\bullet }$?

Individual equations (like 4.15):

$$\begin{array}{rl}{\mathbf{h}}_1& =a[{\beta }_0+{\Omega }_0\mathbf{x}]\\ {\mathbf{h}}_2& =a[{\beta }_1+{\Omega }_1{\mathbf{h}}_1]\\ {\mathbf{h}}_3& =a[{\beta }_2+{\Omega }_2{\mathbf{h}}_2]\\ \mathbf{y}& ={\beta }_3+{\Omega }_3{\mathbf{h}}_3\end{array}$$

One equation (like 4.16):

$$\mathbf{y}={\beta }_3+{\Omega }_{3}a[{\beta }_2+{\Omega }_{2}a[{\beta }_1+{\Omega }_{1}a[{\beta }_0+{\Omega }_0\mathbf{x}]]]$$

Sizes:

• ${\Omega }_0:20\times 5$
• ${\beta }_0:20$
• ${\Omega }_1:10\times 20$
• ${\beta }_1:10$
• ${\Omega }_2:7\times 10$
• ${\beta }_2:7$
• ${\Omega }_3:4\times 7$
• ${\beta }_3:4$

Problem 4.5

Consider a deep neural network with $D_i=5$ inputs, $D_o=1$ output, and $K=20$ hidden layers containing $D=30$ hidden units each. What is the depth of this network? What is the width?

• Depth is 20 (number of hidden layers)
  • Or 21 if we count the output layer? In this case, the definition we’re using is “number of layers with parameters” instead of number of hidden layers
• Width is 30 (number of hidden units in each layer)

Problem 4.6

Consider a network with $D_i=1$ input, $D_o=1$ output, and $K=10$ layers, with $D=10$ hidden units in each. Would the number of weights increase more if we increased the depth by one or the width by one?

Original:

• Input to $h_1$: $10\times 1=10$
• Between 9 hidden layers: $9\times 10\times 10=900$
• Last hidden to output: $10\times 1=10$
• Each hidden layer has 10 biases: $9\times 10=90$
• Output layer: $1$ bias
• Total: $10+900+10+90+1=1011$

Increase depth by 1:

• Input to $h_1$: $10\times 1=10$
• Between 9 hidden layers: $10\times 10\times 10=1000$
• Last hidden to output: $10\times 1=10$
• Each hidden layer has 10 biases: $10\times 10=100$
• Output layer: $1$ bias
• Total: $10+1000+10+100+1=1121$

Increase width by 1:

• Input to $h_1$: $11\times 1=11$
• Between 9 hidden layers: $9\times 11\times 11=1089$
• Last hidden to output: $11\times 1=11$
• Each hidden layer has 10 biases: $9\times 11=99$
• Output layer: $1$ bias
• Total: $11+1089+11+99+1=1211$

Problem 4.7

Choose values for the parameters $\varphi =\{{\varphi }_0,{\varphi }_1,{\varphi }_2,{\varphi }_3,{\theta }_{10},{\theta }_{11},{\theta }_{20},{\theta }_{21},{\theta }_{30},{\theta }_{31}\}$ for the shallow neural network in equation 3.1 (with ReLU activation functions) that will define an identity function over a finite range $x\in [a,b]$.

The function is:

$$\begin{array}{rl}y& =f[x,\varphi ]\\ & ={\varphi }_0+{\varphi }_{1}a[{\theta }_{10}+{\theta }_{11}x]+{\varphi }_{2}a[{\theta }_{20}+{\theta }_{21}x]+{\varphi }_{3}a[{\theta }_{30}+{\theta }_{31}x]\end{array}$$

We want it to be the identity function, such that

$$\begin{array}{rl}y& =f[x,\varphi ]\\ & =x\end{array}$$

If we have:

• ${\varphi }_0=0$
• ${\varphi }_1=1$
• ${\theta }_{10}=0$
• ${\theta }_{11}=1$
• ${\varphi }_2=1$
• ${\theta }_{20}=0$
• ${\theta }_{21}=1$
• ${\varphi }_3=1$
• ${\theta }_{30}=0$
• ${\theta }_{31}=1$

We would get $y=3\cdot \text{ReLU}[x]$, which only equals $x>0$ and has slope $3$ instead of $1$.

Instead, we need

• ${\varphi }_0=a$
• ${\varphi }_1=1$
• ${\theta }_{10}=-a$
• ${\theta }_{11}=1$
• ${\varphi }_2=-1$
• ${\theta }_{20}=-b$
• ${\theta }_{21}=1$
• ${\varphi }_3=0$
• ${\theta }_{30}=0$
• ${\theta }_{31}=1$

which expands to

$$\begin{array}{rl}f[x,\varphi ]& =a+\text{ReLU}[x-a]-\text{ReLU}[x-b]\\ & =a+\text{max}[0,x-a]-\text{max}[0,x-b]\end{array}$$

If we have:

• $x\le a$, both ReLUs are 0 so $f[x]=a$
• $a\le x\le b$, the first ReLU is active, so we have $f[x]=a+(x-a)=x$
• $x\ge b$, both ReLUs are active, so we have $f[x]=a+(x-a)-(x-b)=b$

Problem 4.8

Figure 4.9 shows the activations in the three hidden units of a shallow network (as in figure 3.3). The slopes in the hidden units are $1.0$, $1.0$, and $-1.0$, respectively, and the “joints” in the hidden units are at positions $1/6$, $2/6$, and $4/6$.

• Find values of ${\varphi }_0,{\varphi }_1,{\varphi }_2$, and ${\varphi }_3$ that will combine the hidden unit activations as ${\varphi }_0+{\varphi }_1{h}_1+{\varphi }_2{h}_2+{\varphi }_3{h}_3$ to create a function with four linear regions that oscillate between output values of zero and one. The slope of the leftmost region should be positive, the next one negative, and so on.
• How many linear regions will we create if we compose this network with itself?
• How many will we create if we compose it with itself $K$ times?

Region 1:

• Only $h_3$ is active. Its joint is at $\frac{4}{6}$, so the pre-activation for $h_3(x)$ is $-x+\frac{4}{6}$.
• We need:

$$\begin{array}{rl}y(0)& ={\varphi }_0+{\varphi }_3\left(-0+\frac{4}{6}\right)=0\\ y\left(\frac{1}{6}\right)& ={\varphi }_0+{\varphi }_3\left(-\frac{1}{6}+\frac{4}{6}\right)=1\end{array}$$

• Solving the system of equations gives ${\varphi }_0=4,{\varphi }_3=-6$.

Region 2:

• $h_1$ and $h_3$ are active, which means that the region has a slope of ${\varphi }_1-{\varphi }_3$.
• To get the output back down from $y\left(\frac{1}{6}\right)=1$ to $y\left(\frac{2}{6}\right)=0$, we need a slope of $\frac{-1}{\frac{2}{6}-\frac{1}{6}}=-6$.
• Since we have ${\varphi }_3=-6$, this gives ${\varphi }_1=-12$.

Region 2:

• $h_1$, $h_2,h_3$ are active, so the slope will be ${\varphi }_1+{\varphi }_2-{\varphi }_3$.
• To get the output back up from $y\left(\frac{2}{6}\right)=0$ to $y\left(\frac{4}{6}\right)=1$, we need slope of $\frac{1}{\frac{4}{6}-\frac{2}{6}}=3$.
• Since we have ${\varphi }_1=-12,{\varphi }_3=-6$, we have ${\varphi }_2=9$.

Region 4:

• $h_1$ and $h_2$ are active, so the slope will be ${\varphi }_1+{\varphi }_2$.
• To get the output down from $y\left(\frac{4}{6}\right)=1$ to $y(1)=0$, we need a slope of $\frac{-1}{1-\frac{4}{6}}=-3$.
• We already achieve this with ${\varphi }_1=-12$ an ${\varphi }_2=-9$.

If we compose the network with itself once, we will get $4^2=16$ regions; each region in the second network is replicated four times.

If we compose the network with itself $K$ times, we will get $4^{K+1}$ regions.

Problem 4.9

Following problem 4.8, is it possible to create a function with three linear regions that oscillates back and forth between output values of zero and one using a shallow network with two hidden units? Is it possible to create a function with five linear regions that oscillates in the same way using a shallow network with four hidden units?

It is not possible to create a function with three linear regions that oscillates back and forth between output values of 0 and 1 using a shallow network with two hidden units. At best it can rise and fall once, producing only two linear pieces with opposite slopes.

• Each hidden ReLU unit can change the output slope once—at the joint where that ReLU switches on or off.
• for 0-1-0-1 (or $+-+$), we would need two segments that have positive slope, but this isn’t possible because a ReLU only activates once, so the positive hidden unit can only turn on/off once.
• Because one unit’s jump adds a positive amount to the slope and the other unit’s jump subtracts a positive amount, the slope can go up-then-down, down-then-up, but never up-down-up (two flips) or down-up-down.

However, it is possible to create a function with five linear regions that oscillates in the same way using a shallow network with four hidden units, and generally, for $N\ge 3$ hidden units it’s possible to make a function that oscillates back and forth $N+1$ times.

• Four units provide four independent slope jumps, letting you enforce the sign pattern $+-+-+$.
• That yields five alternating linear pieces $0\to 1\to 0\to 1\to 0\to 1$, so the five-region oscillation is achievable with a shallow network that has four hidden units.

Problem 4.10

Consider a deep neural network with a single input, a single output, and $K$ hidden layers, each of which contains $D$ hidden units. Show that this network will have a total of $3D+1+(K-1)D(D+1)$ parameters.

• Input to first hidden layer has $D$ weights and $D$ biases – $2D$
• Between hidden layers we connect $D$ units to $D$ units
  • $D^2$ weights, $D$ biases
  • This happens $K-1$ times
  • Total: $(K-1)(D^2+D)$
• Last hidden layer and output: $D$ weights and $1$ bus – $1D+1$

Total:

$$3D+1+(K-1)(D^2+D)$$

which is the same thing as $3D+1+(K-1)D(D+1)$.

Problem 4.11

Consider two neural networks that map a scalar input $x$ to a scalar output $y$. The first network is shallow and has $D=95$ hidden units. The second is deep and has $K=10$ layers, each containing $D=5$ hidden units. How many parameters does each network have? How many linear regions can each network make (see equation 4.17)? Which would run faster?

The first network has:

$$3\cdot 95+1=286\text{ parameters}$$

The second network has:

$$(3\cdot 5)+1+(10-1)(5^{2+5)}=286\text{ parameters}$$

For the shallow network, since there is just one input, each hidden unit creates one joint, for a total of 95 joints separating 96 linear regions.

The number of linear regions for the deep network is given by equation 4.17:

$$N_r={\left(\frac{D}{D_i}+1\right)}^{D_i(K-1)}\cdot \sum _{j=0}^{D_i}\left(\genfrac{}{}{0ex}{}{D}{j}\right)=60,466,176$$

In principle, the shallow network will be faster to run on modern hardware as the computation is more parallel.