The universal approximation theorem states that for any continuous function, there exists a shallow network that can approximate this function to any specified precision.
Let’s say we have a shallow neural network of the form:
where -th hidden unit is:
where is an activation function such as ReLU. We can then write the neural network as:
The number of hidden units in a shallow network is a measure of the network capacity.
With ReLU activation functions, the output of a network with hidden units has at most D “joints” and so is a piecewise linear function with at most linear regions:
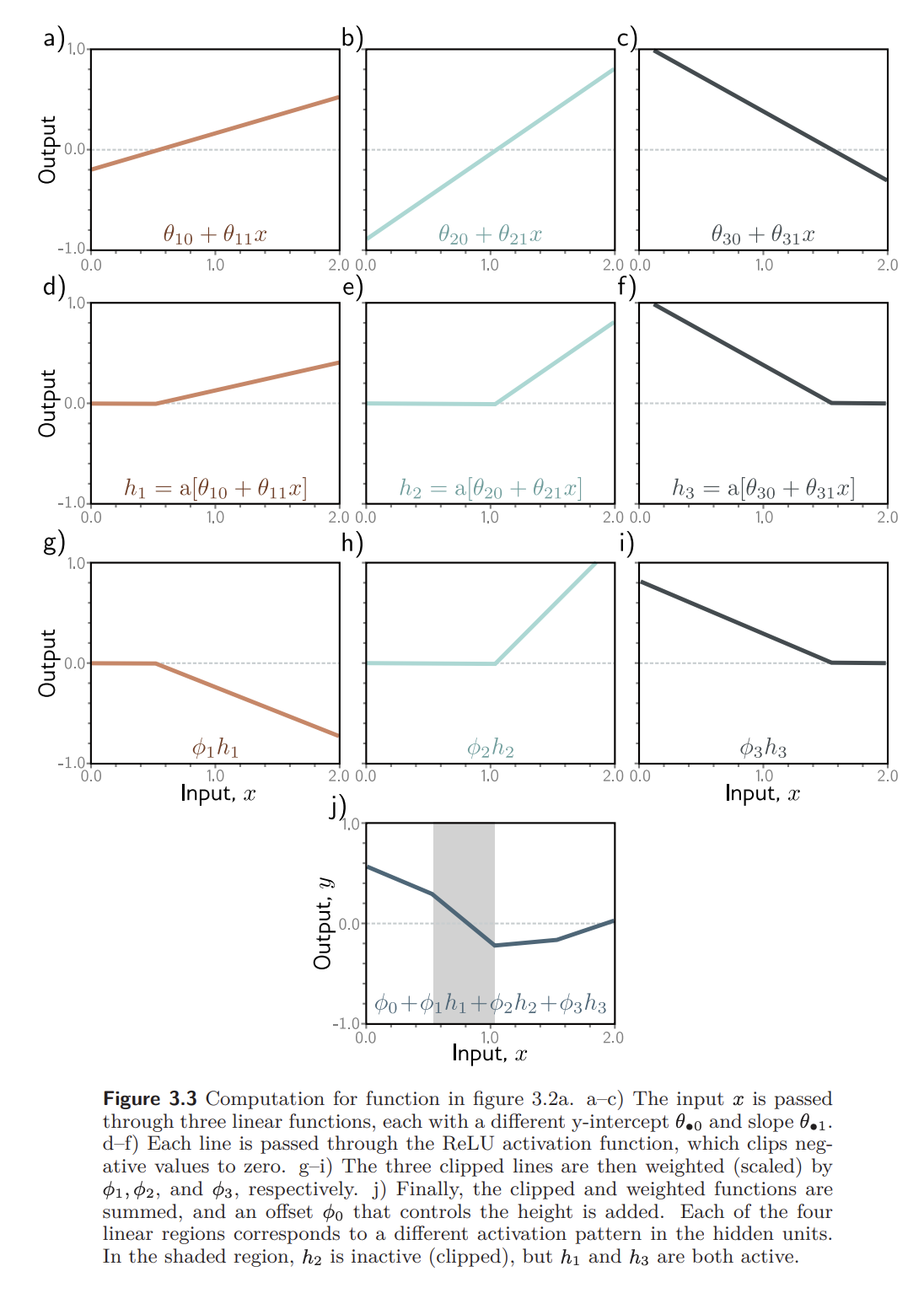
As we add more hidden units, the model can approximate more complex functions. With enough capacity (more hidden units), a shallow network can describe any continuous 1D function defined on a compact subset of the real line to arbitrary precision.
To see this, consider that every time we add a hidden unit, we add another linear region to the function. More regions means that each represents smaller sections of the function, which in turn means a better approximation.
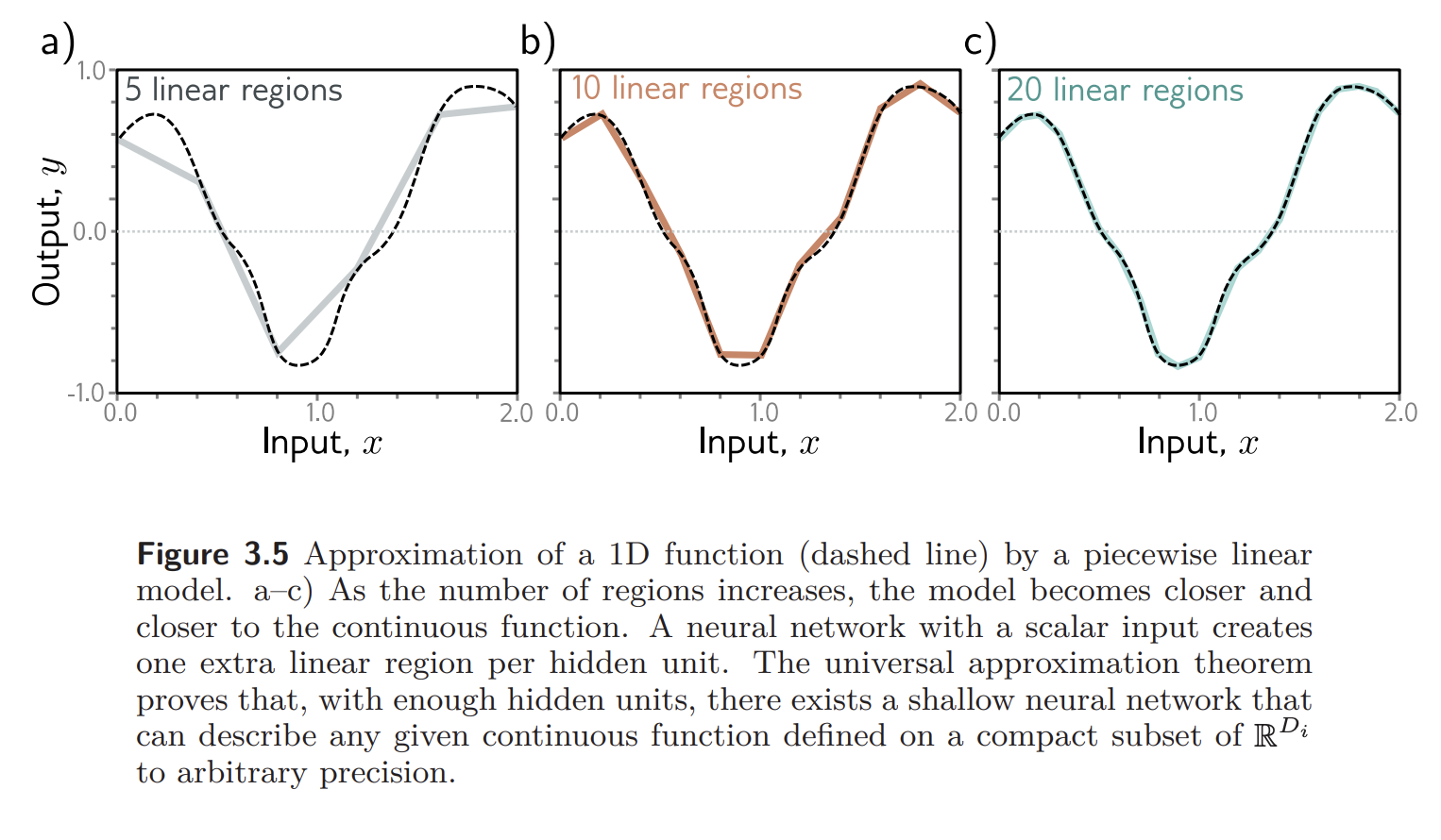
Why would we ever need a neural network with more than one hidden layer? The theorem guarantees existence, but no claims about the scaling of (the number of hidden neurons) as a function of , the desired approximation error. might grow exponentially as get smaller.
Width Version
The width version of this theorem states that there exists a network with one hidden layer containing a finite number of hidden units that can approximate any specified continuous function on a compact subset of to arbitrary accuracy.
Depth Version
There exist a network with ReLU activation functions and at least hidden units in each layer that can approximate any -dimensional Lebesgue integrable function to arbitrary accuracy given enough layers. This was shown in [1709.02540] The Expressive Power of Neural Networks: A View from the Width.
This is known as the depth version of the universal approximation theorem.
Formalization
Universal Approximation Theorem
Let be any continuous sigmoidal function. The finite sums of the form
- ( are weights and are biases)
are dense in (continuous functions in domain ).
In other words, given any and , there is a sum , of the above form, for which
In this example, . It just needs to be a compact domain.
Sigmoidal function
A function is “sigmoidal” if
Informal Proof
Suppose we let for , then
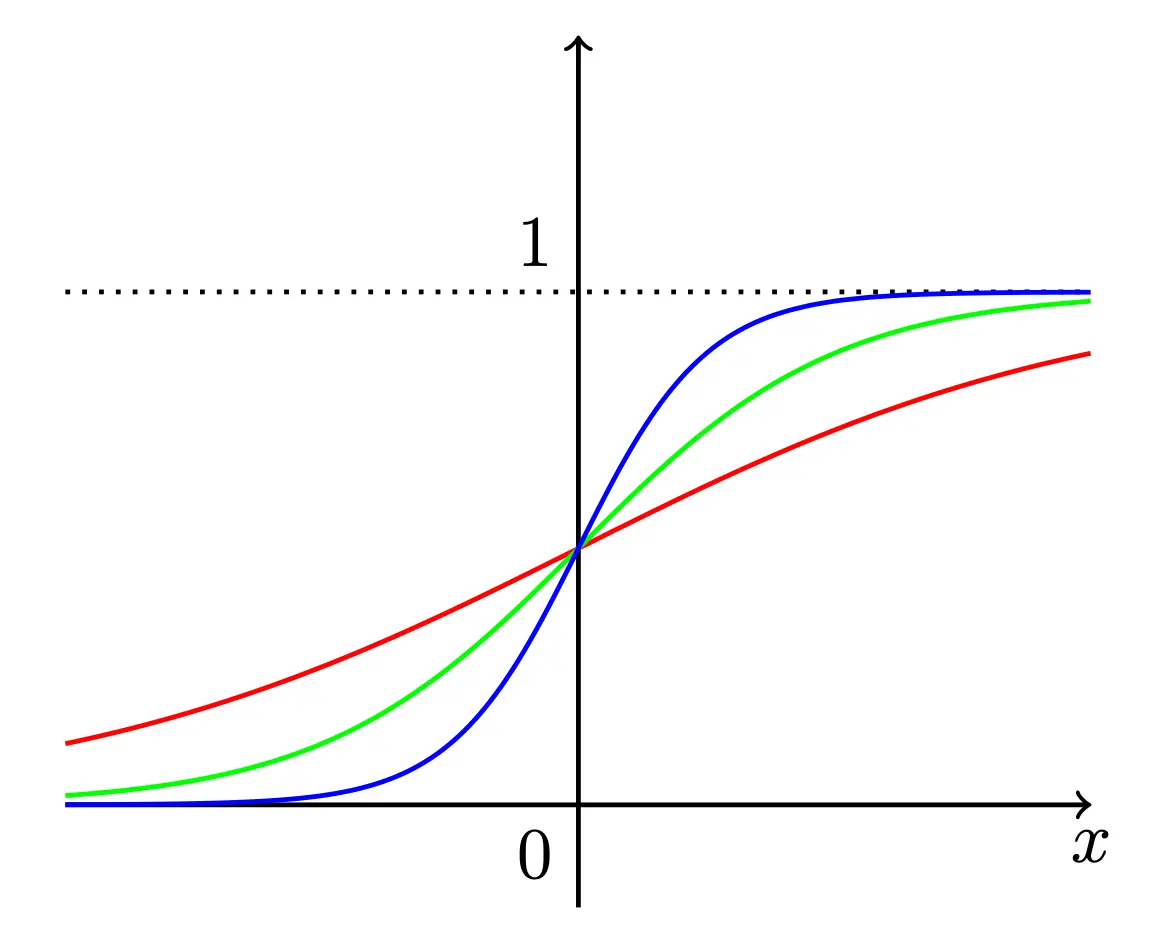
By shifting the -axis by , we get
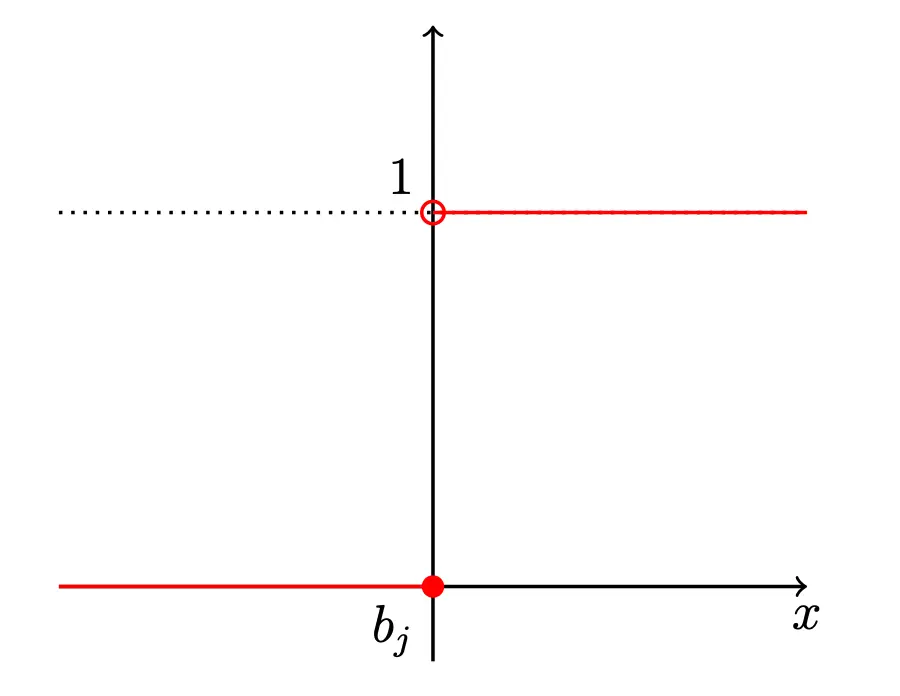
Within this limit, we obtain the Heaviside step function:
Let us define
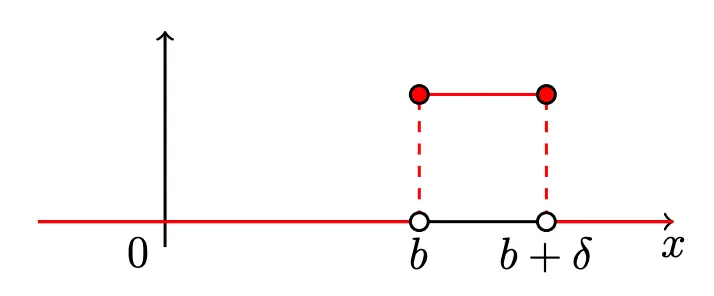
We can use two such functions to create a horizontal piece:
where is made from sigmoidal functions:
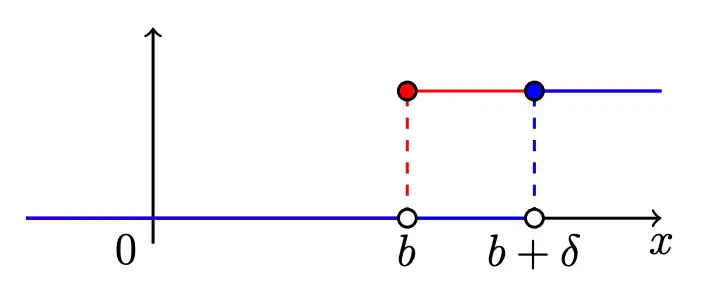
The piece function is defined as
Since is continuous,
Therefore, an interval, , such that
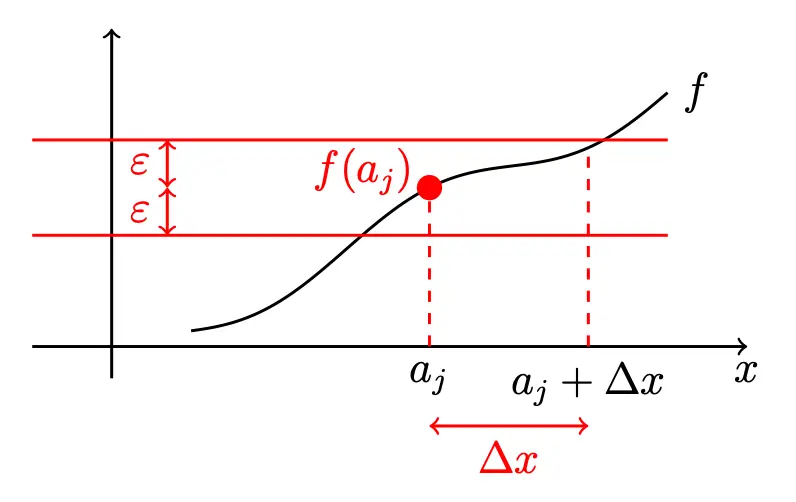
As a result, the function
satisfies the constraint
Here, is the number of subintervals. can also be written in terms of threshold functions (which can be approximated by sigmoids) as:
Thus, the total number of hidden neurons required to construct is .
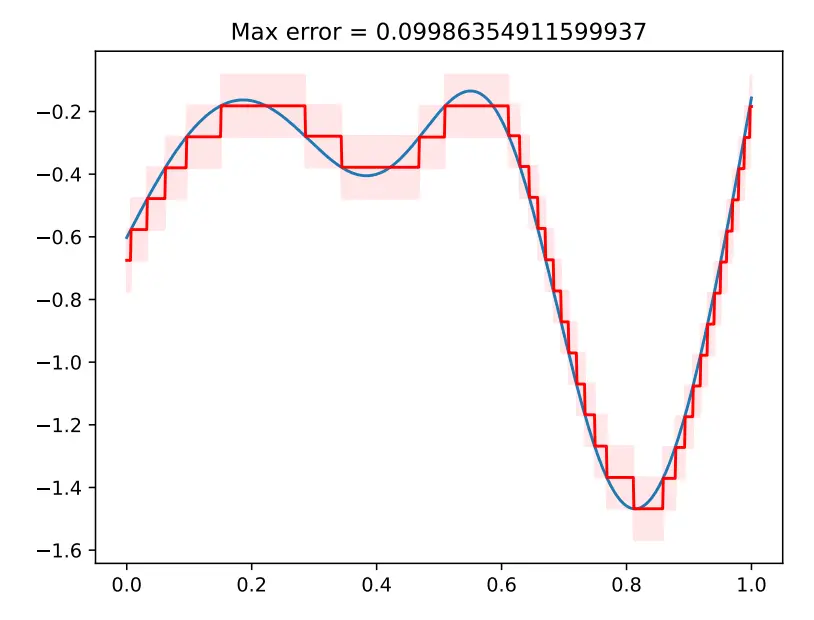
Instead of using sigmoid, we can do ReLU, etc. The proof would be different but in theory the result should be the same.