Deep Neural Network

We have seen that composing shallow networks can give us complex functions. We can extend this to construct deep networks with more than two hidden layers; modern networks have hundreds of layers with thousands of hidden units at each layer.

• The number of hidden units in each layer is referred to as the width of the network
• The number of hidden layers is the depth
• The total number of hidden units is a measure of network capacity

Hyperparameters

We denote the number of layers as $K$ and the number of hidden units in each layer as $D_1,D_2,\dots ,D_K$. These are examples of hyperparameters. They are quantities chosen before we learn the model parameters (i.e., the slope and intercept terms). For fixed hyperparameters (e.g., $K=2$ and $D_k=3$ hidden units each), the model describes a family of functions, and the parameters determine the particular function. Hence, when we also consider the hyperparameters, we can think of neural networks as representing a family of families of functions relating input to output.

General Formulation

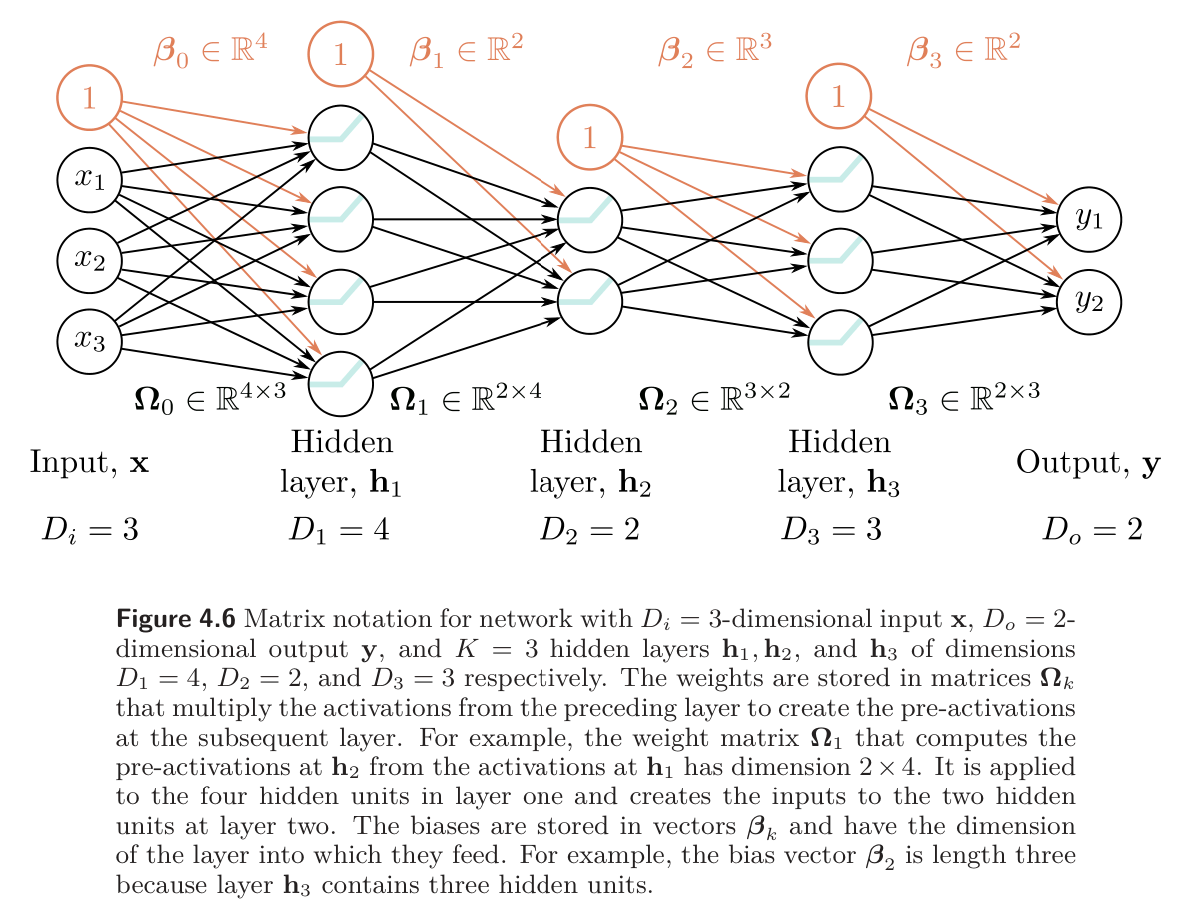
• See Matrix Notation for an introduction to matrix notation for a simple composition of shallow networks

We describe the vector of hidden units at layer $k$ as ${\mathbf{h}}_k$, the vector of biases (intercepts) that contribute to hidden layer $k+1$ as ${\beta }_k$, and the weights (slopes) that are applied to the $k$-th layer and contribute to the $(k+1)$-th layer as ${\Omega }_k$. A general deep network $\mathbf{y}=\mathbf{f}[\mathbf{x},\varphi ]$ with $K$ layers can now be written as:

$$\begin{array}{rl}{\mathbf{h}}_1& =a[{\beta }_0+{\Omega }_0\mathbf{x}]\\ {\mathbf{h}}_2& =a[{\beta }_1+{\Omega }_1{\mathbf{h}}_1]\\ {\mathbf{h}}_3& =a[{\beta }_2+{\Omega }_2{\mathbf{h}}_2]\\ & ⋮\\ {\mathbf{h}}_K& =a[{\beta }_{K-1}+{\Omega }_{K-1}{\mathbf{h}}_{K-1}]\\ \mathbf{y}& ={\beta }_K+{\Omega }_K{\mathbf{h}}_K\end{array}$$

The parameters $\varphi$ of this model comprise all of these weight matrices and bias vectors $\varphi =\{{\beta }_k,{\Omega }_k{\}}_{k=0}^K$.

• If the $k$-th layer has $D_k$ has hidden units, then the bias vector ${\beta }_{k-1}$ will be of size $D_k$. The last bias vector ${\beta }_K$ has the size $D_o$ of the output.
• The first weight matrix ${\Omega }_0$ has size $D_1\times D_i$ where $D_i$ is the size of the input.
• The last weight matrix ${\Omega }_K$ is $D_o\times D_K$, and the remaining matrices ${\Omega }_k$ are $D_{k+1}\times D_k$

We can equivalently write the network as a single function:

$$\mathbf{y}={\beta }_K+{\Omega }_K[{\beta }_{K-1}+{\Omega }_{K-1}a[\dots {\beta }_2+{\Omega }_{2}a[{\beta }_1+{\Omega }_{1}a[{\beta }_0+{\Omega }_0\mathbf{x}]]\dots ]]$$

In diagram form: