We saw from Sources of Test Error and Mathematical Formulation of Test Error that test error results from noise, bias, and variance.
Noise is insurmountable; there is nothing we can do to circumvent this, and it represents a fundamental limit on expected model performance. However, it is possible to reduce the two other terms.
Reducing variance
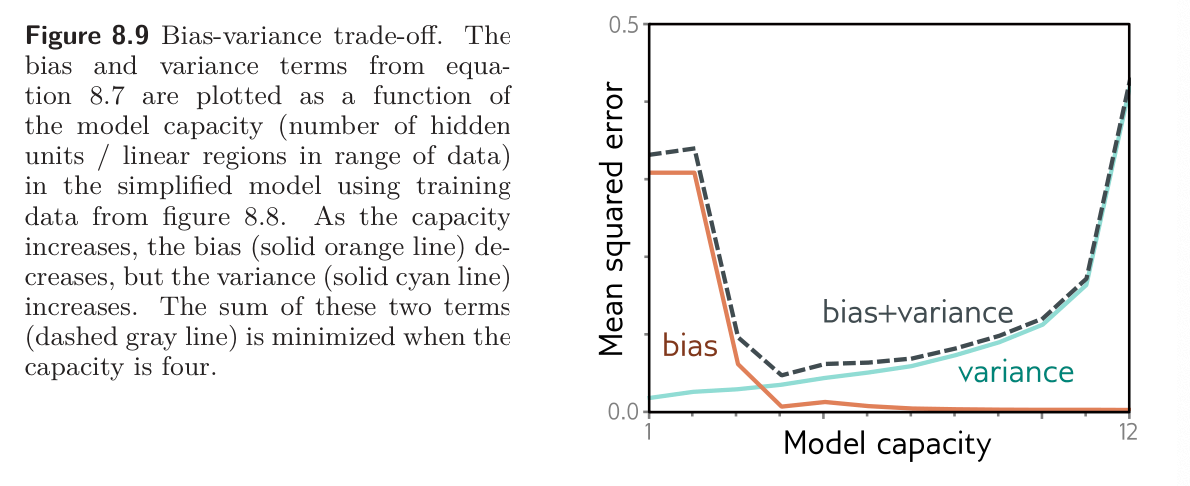
Recall that the variance results from limited noisy training data. Fitting the model to two different training sets results in slightly different parameters. It follows that we can reduce the variance by increasing the amount of training data. This averages out the inherent noise and ensures that the input space is well sampled.
The figure below shows the effect of training with 6, 10, and 100 samples. For each dataset size, we show the best-fitting model for three training datasets. With only six samples, the fitted function is quite different each time; the variance is significant. As we increase the number of samples, the fitted models become very similar, and the variance reduces. In general, adding training data almost always improves test performance.
Reducing bias
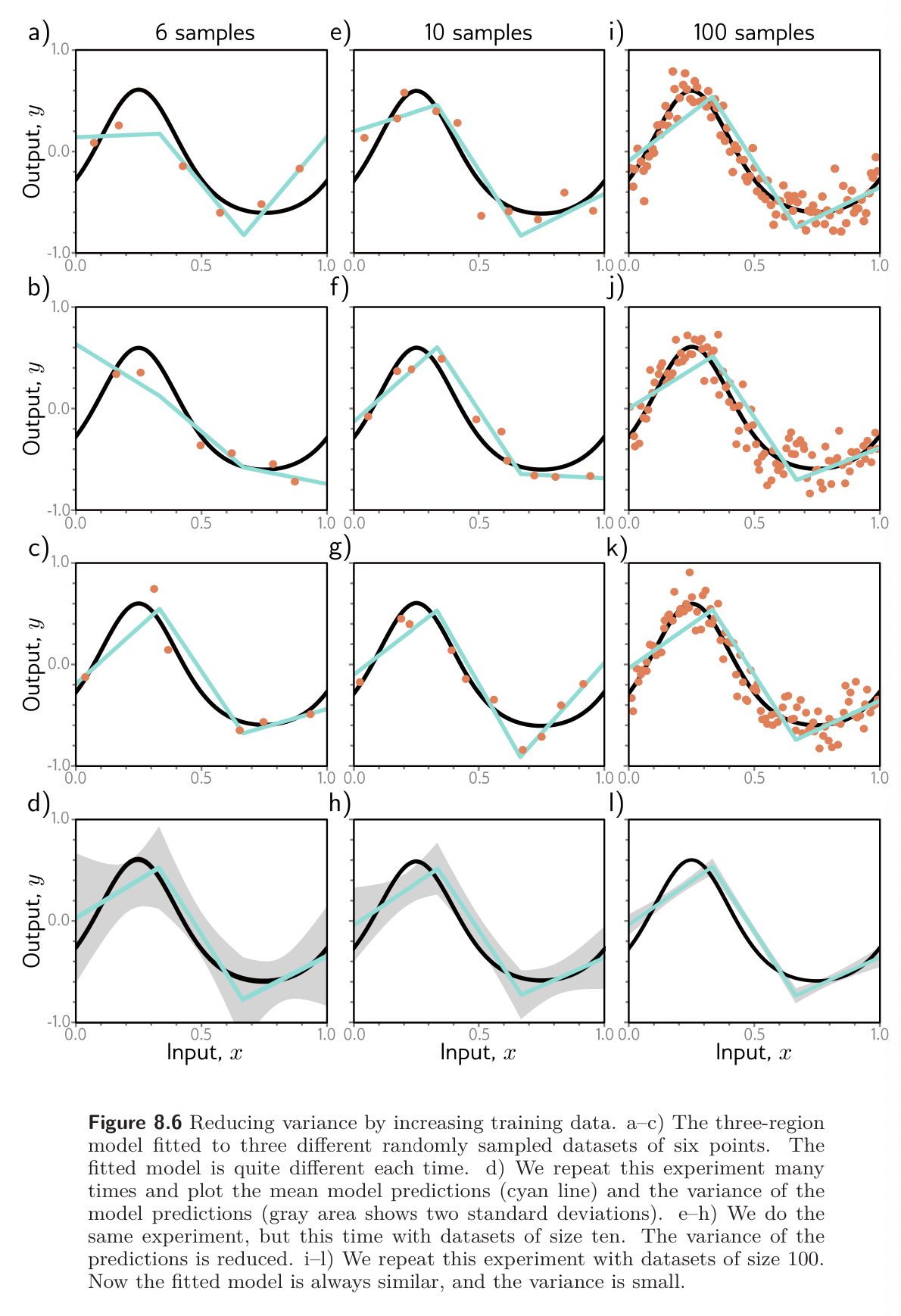
The bias term results from the inability of the model to describe the true underlying function. We can reduce this error by making the model more “flexible”; this is done by increasing model capacity. For neural networks, this means adding more hidden units/layers.
In the simplified model, adding more capacity corresponds to adding more hidden units so that the interval is divided into more linear regions. Part a-c in the figure below shows that this does indeed reduce the bias; as we increase the number of linear regions from 3 to 10, the model becomes flexible enough to fit the true function closely.
Bias-Variance Tradeoff
However, parts d-f of the figure above shows an unexpected side-effect of increasing model capacity. For a fixed-size training dataset, the variance term typically increases as the model capacity increases. Consequently, increasing the model capacity does not necessarily reduce the test error; this is known as bias-variance tradeoff.
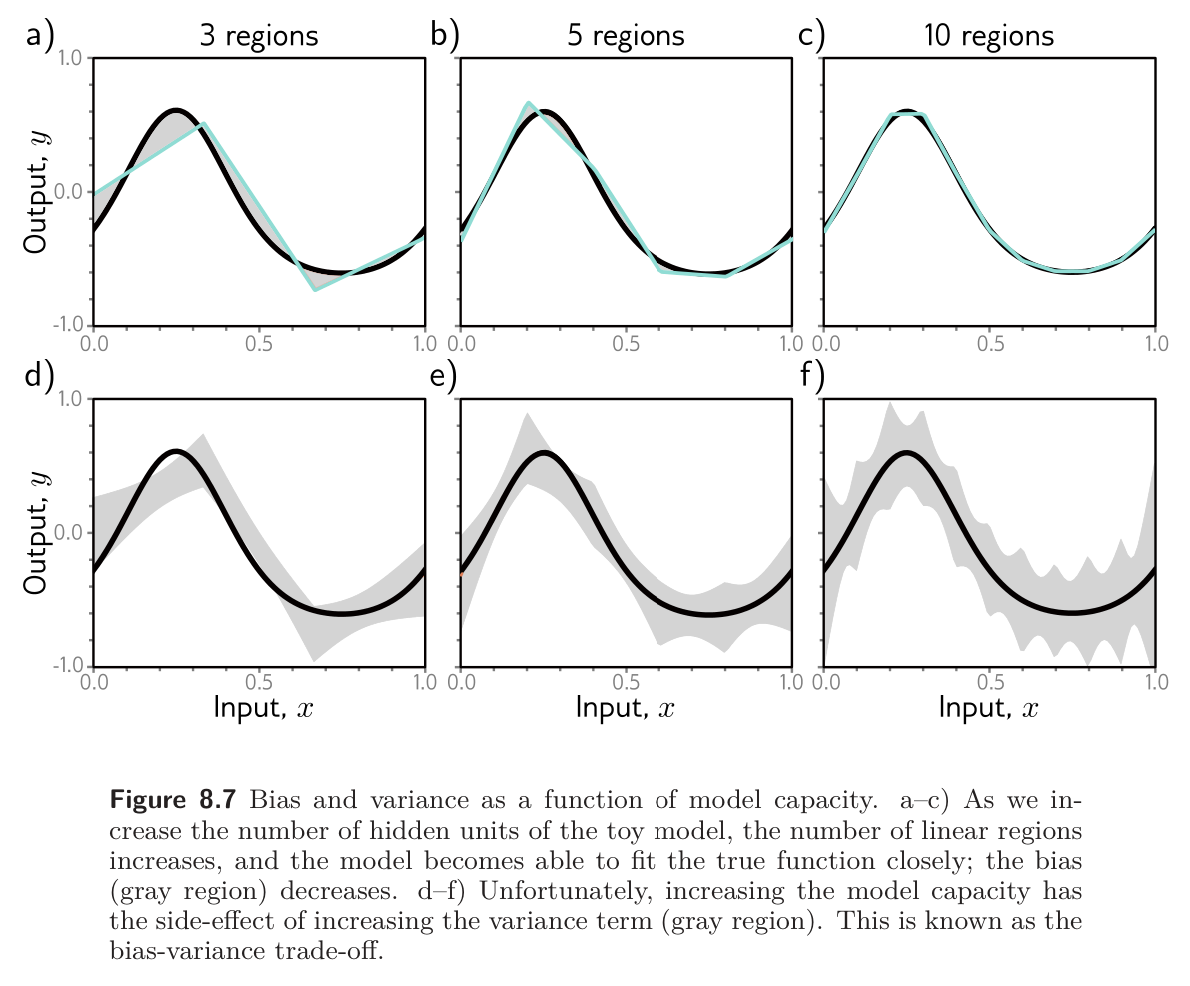
This is explored the figure below.
- In panels a-c, we fit the simplified three-region model to 3 different datasets of 15 points. Although the datasets differ, the final model is much the same; the noise in the dataset roughly averages out in each linear regions.
- In panels d-f, we fit the model with 10 regions to the same three datasets. This model has more flexibility, but this is disadvantageous; the model certainly fits the data better, and the training error will be lower, but much of the extra descriptive power is devoted to modeling the noise. This is known as overfitting.
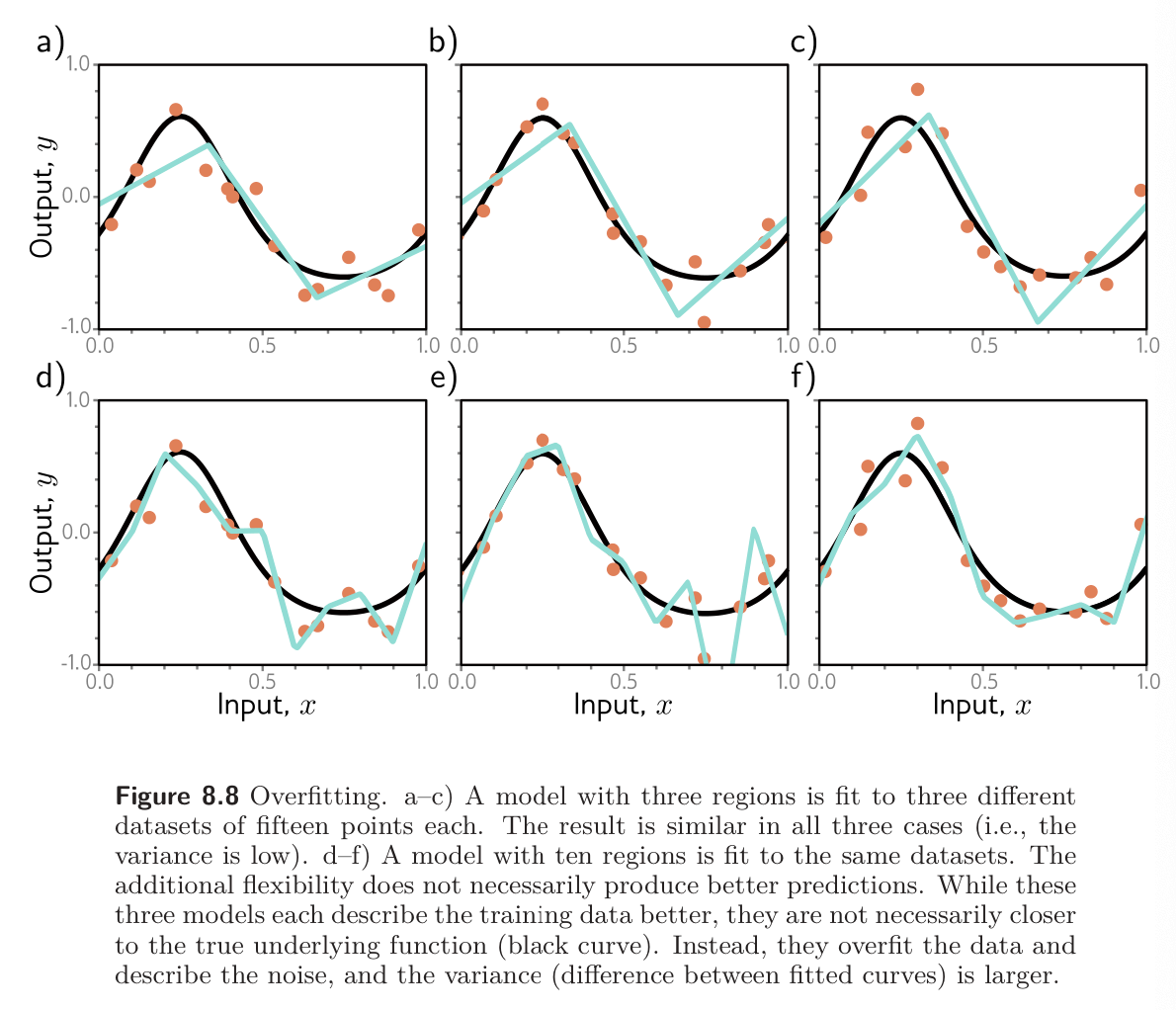
Adding capacity to a model decreases bias but increases variance for a fixed-size training dataset. This suggests an optimal capacity where the bias is not too large and the variance is still relatively small. The figure below shows how these terms vary numerically for the toy model as increase the capacity, using the data from figure 8.8. For regression models, the total expected error is the sum of the bias and the variance, and this sum is minimized, and this sum is minimized when the model capacity is four (4 hidden units and 4 hidden linear regions in the range of the data).