L2 Regularization

The L2 penalty is the sum of squares of the weights, represented mathematically as:

$$\lambda \sum w_i^2$$

Or, more generally:

$$\hat{\varphi }=\underset{\varphi }{\mathrm{argmin}}\left[\sum _{i=1}^I{\ell }_i[{\mathbf{x}}_i,{\mathbf{y}}_i]+\lambda \sum _j{\varphi }_j^2\right]$$

where $j$ indexes the parameters. This is also as Tikhonov regularization or Ridge Regression, or (when applied to matrices) Frobenius norm regularization.

For neural networks, L2 regularization is usually applied to the weights but not the biases and is hence referred to as a weight decay term. The effect is to encourage smaller weights, so the output function is smoother.

• Why is the output function smoother? To see this, consider that the output prediction is a weighted sum of the activations at the last hidden layer. If the weights have a smaller magnitude, the output will vary less. The same logic applies to the computation of the pre-activations at the last hidden layer and so on, progressing throughout the network. In the limit, if we forced all the weights to be zero, the network would produce a constant output determined by the final bias parameter.

L2 penalty tends to shrink the weights, but does not necessarily set them to zero. This can lead to models where the influence of each feature is small but not eliminated, resulting in a more distributed, and often more stable, set of weights.

L2 regularization is smooth and differentiable, and hence it’s easier to handle in optimization algorithms, such as gradient descent.

The figure below shows the effect of fitting a simple network with weight decay and different values of the regularization coefficient $\lambda$.

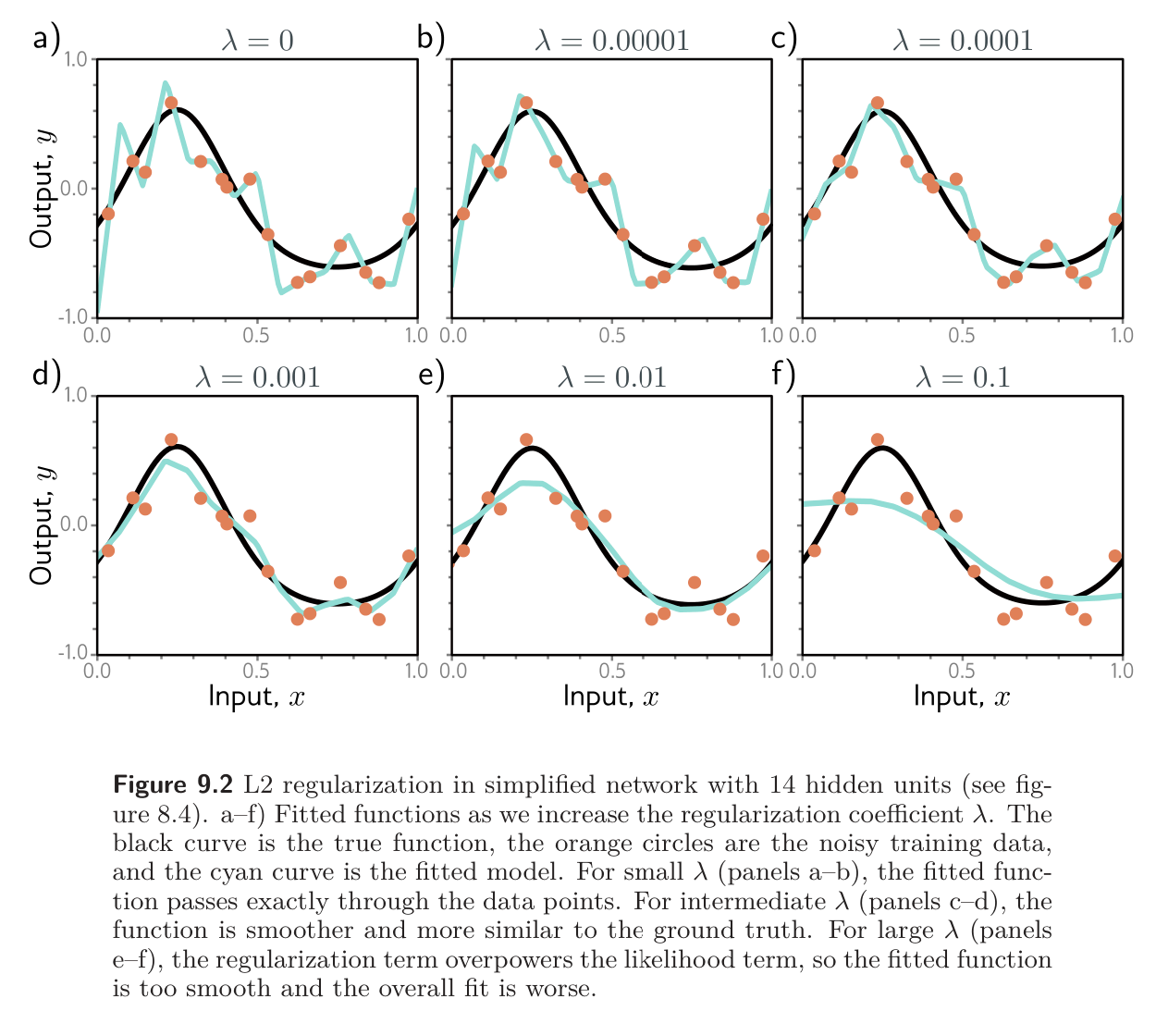
When $\lambda$ is small, it has little effect. However, as $\lambda$ increases, the fit to the data becomes less accurate, and the function becomes smoother. This might improve the performance for two reasons:

• If the network is overfitting, then adding regularization means the network must trade off adherence to the data against the desire to be smooth. Error due to variance reduces (the model no longer needs to pass through every data point)
• When the network is over-parameterized, some of the extra model capacity describes areas with no training data. The regularization term will favour functions that smoothly interpolate between the nearby points. This is reasonable behavior in the absence of knowledge about the true function.