Mergesort

Python implementation here: implementations/sorting-algorithms/mergesort.py

Recursive algorithms reduce large problems into smaller ones. Mergesort is a recursive approach to sorting that involves partitioning the elements into two groups, sorting each of the smaller problems recursively, and then interleaving the two sorted lists to totally order the elements.

$$\begin{array}{rl}\text{Mergesort}& (A[1,\dots ,n])\\ & \text{Mergesort}(\text{MergeSort}(A[1,\dots ,\lfloor n/2\rfloor ]),\text{Mergesort}(A[\lfloor n/2\rfloor +1,n])\end{array}$$

The base case for the recursion occurs when the subarray to be sorted consists of one element, so no re-arrangement is necessary.

The efficiency of mergesort depends upon how efficiently we can combine the two sorted halves into a single sorted list. We could concatenate them into one list and call heapsort or some other sorting algorithm to do it, but that would just destroy all the work spent sorting our component lists.

Merging

Instead, we merge the two lists together.

Observe that the smallest overall item in two lists sorted in increasing order must sit at the top of one of those lists. This smallest element is removed, leaving two sorted lists behind – one slightly shorter than before. The second smallest item overall must now be atop one of these lists. Repeating this operation until both lists are empty will merge two sorted lists (with a total of $n$ elements between them) into one, using at most $n-1$ comparisons or $O(n)$ total work.

Complexity

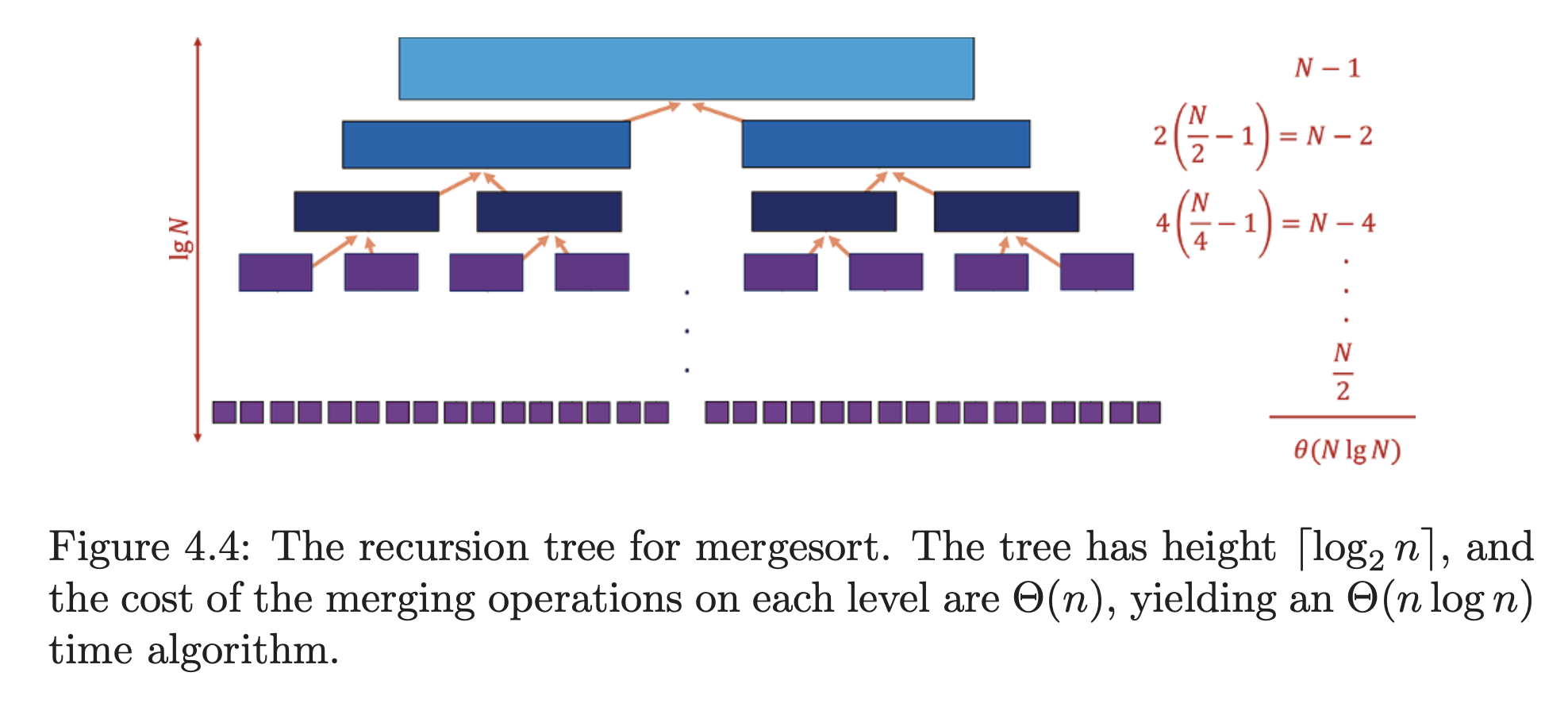
\What is the total running time of mergesort? It helps to think about how much work is done at each level of the execution tree.

If we assume for simplicity that $n$ is a power of two, the $k$-th level consists of all the $2^k$ calls to mergesort processing subranges of $n/2^k$ elements.

In general, the work done on the $k$-th level involves merging $2k$ pairs of sorted lists, each of size $n/2^k+1$, for a total of at most $n-2^k$ comparisons.

• The work done on the $k=0$ level (the top) involves merging 1 pair of sorted lists, each of size $n/2$, for a total of at most $n-1$ comparisons.
• The work done on the $k=1$ level (one down) involves merging 2 pairs of sorted lists, each of size $n/4$, for a total of at most $n-2$ comparisons.

Linear work is done merging all the elements on each level. Each of the $n$ elements appears in exactly one subproblem on each level. The most expensive case (in terms of comparisons) is actually the top level.

The number of elements in a subproblem gets halved at each level. The number of times we can halve $n$ until we get to 1 is $\lg n$. Because the recursion goes $\lg n$ levels deep, and a linear amount of work is done per level, mergesort takes $O(n\log n)$ time in the worst case.

Notes

Mergesort is a great algorithm for sorting linked lists, because it does not rely on random access to elements like heapsort and quicksort.

Its primary disadvantage is the need for an auxiliary buffer when sorting arrays. It is easy to merge two sorted linked lists without using any extra space, just by rearranging the pointers. However, to merge two sorted arrays (or portions of an array), we need to use a third array to store the result of the merge to avoid stepping on the component arrays.

Mergesort is a classic divide-and-conquer algorithm. We are ahead of the game whenever we can break one large problem into two smaller problems, because the smaller problems are easier to solve. The trick is taking advantage of the two partial solutions to construct a solution of the full problem, as we did with the merge operation.

Implementation

The divide-and-conquer mergesort routine follows naturally from the pseudocode:

void merge_sort(item_type s[], int low, int high) {
	int middle; /* index of middle element */ 
	if (low < high) { 
		middle = (low + high) / 2; 
		merge_sort(s, low, middle); 
		merge_sort(s, middle + 1, high); 
		
		merge(s, low, middle, high); 
	} 
}

More challenging turns out to be the details of how the merging is done. The problem is that we must put our merged array somewhere. To avoid losing an element by overwriting it in the course of the merge, we first copy each subarray to a separate queue and merge these elements back into the array. In particular:

void merge(item_type s[], int low, int middle, int high) {
	int i; /* counter */ 
	queue buffer1, buffer2; /* buffers to hold elements for merging */ 
	
	init_queue(&buffer1); 
	init_queue(&buffer2); 
	
	for (i = low; i <= middle; i++) enqueue(&buffer1, s[i]); 
	for (i = middle + 1; i <= high; i++) enqueue(&buffer2, s[i]); 
	
	i = low; 
	
	while (!(empty_queue(&buffer1) || empty_queue(&buffer2))) { 
		if (headq(&buffer1) <= headq(&buffer2)) { 
			s[i++] = dequeue(&buffer1);
		} else { 
			s[i++] = dequeue(&buffer2); 
		} 
	} 
	
	while (!empty_queue(&buffer1)) { 
		s[i++] = dequeue(&buffer1); 
	} 
	
	while (!empty_queue(&buffer2)) { 
		s[i++] = dequeue(&buffer2); 
	} 
}