Sorting Algorithm Lower Bounds

We have seen several sorting algorithms (Heapsort, Mergesort) that run in worst case $O(n\log n)$ time, but none that are linear. To sort $n$ items certainly requires looking at all of them, so any algorithm must be $\Omega (n)$ in the worst case.

Is sorting be possible in linear time? The answer is no, presuming that your algorithm is based on comparing pairs of elements.

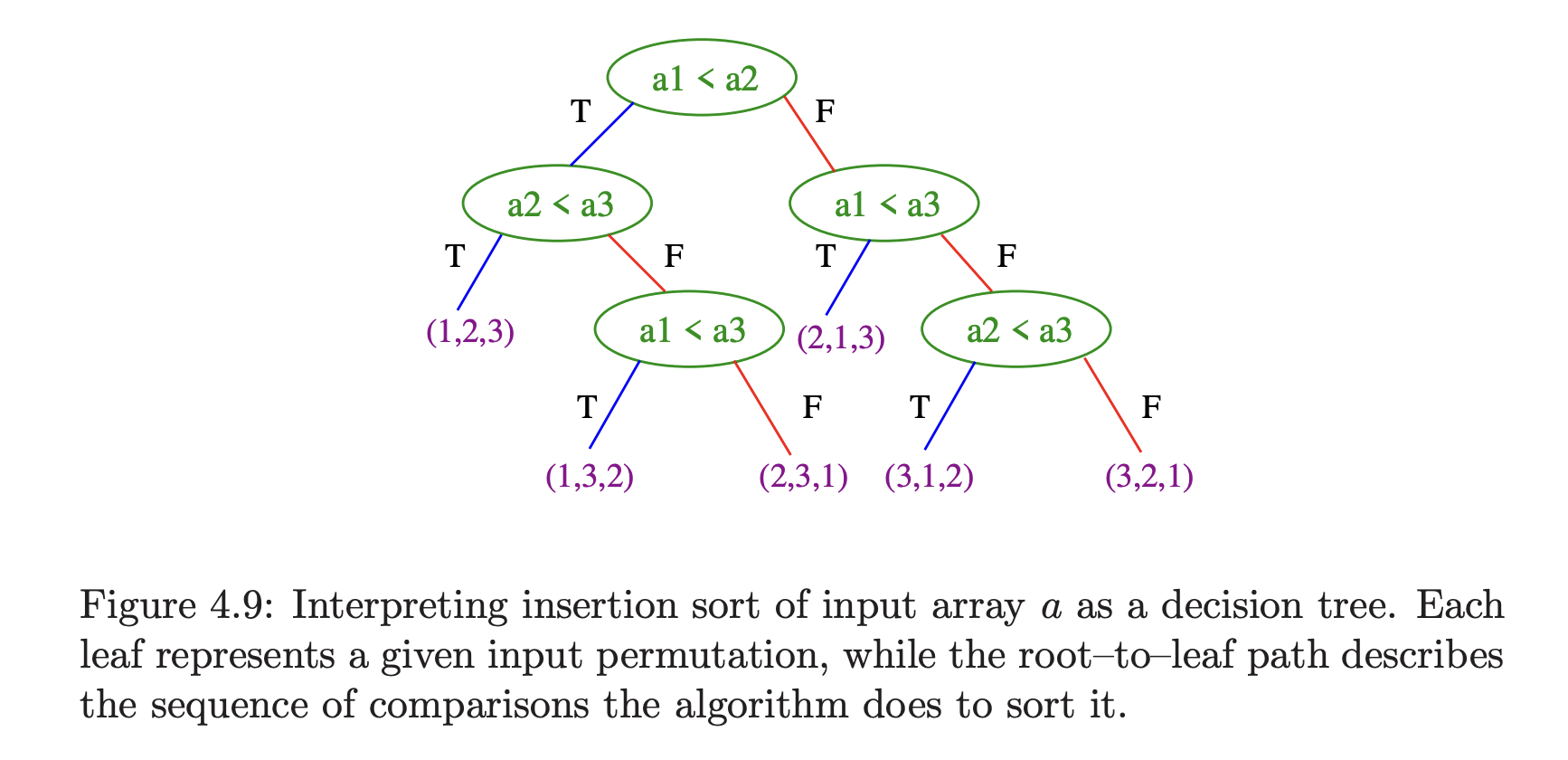
An $\Omega (n\log n)$ lower bound can be shown by observing that any sorting algorithm must behave differently during execution on each of the $n!$ possible permutations of $n$ keys. If an algorithm did exactly the same thing with two different input permutations, there is no way that both of them could correctly come out sorted. The outcome of each pairwise comparison governs the run-time behavior of any comparison-based sorting algorithm. We can think of the set of all possible executions for such an algorithm as a tree with $n!$ leaves, each of which correspond to one input permutation, and each root–to–leaf path describes the comparisons performed to sort the given input. The minimum height tree corresponds to the fastest possible algorithm, and it happens that $\lg (n!)=\Theta (n\log n)$.

The figure below presents the decision tree for insertion sort on three elements. Consider the input $(3,1,2)$. Because $a_1\ge a_2$, these elements must be swapped to produce a sorted order. Insertion sort then compares the end of the sorted array (the original input $a_1$) against $a_3$. If $a_1\ge a_3$, the final test of $a_3$ against the head of the sorted part (original input $a_2$) decides whether to put $a_2$ first or second in sorted order.

This lower bound is important for several reasons. The idea can be extended to give lower bounds for many applications of sorting, including element uniqueness, finding the mode, and constructing convex hulls.

Sorting has one of the few non-trivial lower bounds among algorithmic problems.

Note that hashing-based algorithms do not perform such element comparisons, putting them outside the scope of this lower bound. But hashing-based algorithms can get unlucky, and with worst-case luck the running time of any randomized algorithm for one of these problems will be $\Omega (n\log n)$.