Quicksort

When implemented well, quicksort is typically two to three times faster than mergesort or heapsort.

Suppose we select an arbitrary item $p$ from the $n$ items we seek to sort. Quicksort separates the $n-1$ other items into two piles: a low pile containing all the elements that are $<p$, and a high pile containing all the elements that are $\ge p$. Low and high denote the array positions into which we place the respective piles, leaving a single slot between them for $p$.

Such partitioning buys as two things:

1. The pivot element $p$ ends up in the exact array position it will occupy in the final sorted order.
2. Second, after partitioning no element flips to the other side in the final sorted order.

Thus, we can now sort the elements to the left and the right of the pivot independently! This gives us a recursive sorting algorithm, since we can use the partitioning approach to sort each subproblem. The algorithm must be correct, because each element ultimately ends up in the proper position:

void quicksort(item_type array[], int low, int high) { 
	int partitionIndex; /* index of partition */ 
	
	if (low < high) { 
		partitionIndex = partition(array, low, high); 
		quicksort(array, low, partitionIndex - 1); 
		quicksort(array, partitionIndex + 1, high); 
	} 
}

We can partition the array in one linear scan for a particular pivot element by maintaining three sections:

• Less than the pivot (to the left of firsthigh)
• Greater than or equal to the pivot (between firsthigh and i)
• Unexplored to the right of `i

int partition(item_type array[], int low, int high) {      
	int i; /* loop counter */      
	int pivotIndex; /* pivot element index */      
	int firstHighIndex; /* divider position for pivot element */
	
	pivotIndex = high; /* select last element as pivot */
	firstHighIndex = low;
	
	for (i = low; i < high; i++) {
		if (array[i] < array[pivotIndex]) {
			swap(&array[i], &array[firstHighIndex]);
			firstHighIndex++;
		}
	}           
	
	swap(&array[pivotIndex], &array[firstHighIndex]);
	
	return firstHighIndex;
}

• Python implementation here: implementations/sorting-algorithms/quicksort.py.

Complexity

Since the partitioning step consists of at most $n$ swaps, it takes linear time. Quicksort, like Mergesort, builds a recursion tree of nested subranges of the $n$-element array Like mergesort, quicksort spends linear time processing (now withpartition instead of merge) the elements in each subarray on each level. As with mergesort, quicksort runs in $O(n\cdot h)$ time, where $h$ is the height of the recursion tree. The difficulty is that the height of the tree depends upon where the pivot element ends up in each partition.

If we get very lucky and happen to repeatedly pick the median element as our pivot, the subproblems are always half the size of those at the previous level. The height represents the number of times we can halve $n$ until we get to 1, meaning $h=\lfloor \lg n\rfloor$. This corresponds to the best case of quicksort and is shown below.

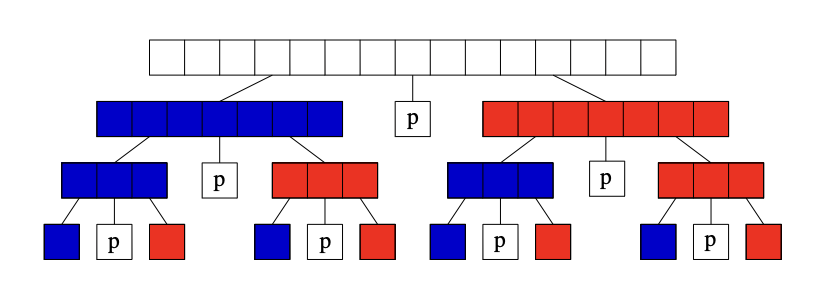
The worst case is we get consistently unlucky and our pivot element always splits the array as unequally as possible. This implies that the pivot element is always the biggest or smallest element in the sub-array. After this pivot settles into its position, we will be left with one subproblem of size $n-1$. After doing linear work we have reduced the size of our problem by just one measly element. It takes a tree of height $n-1$ to chop our array down to one element per level, for a worst case time of $\Theta (n^2)$.

Average Case

Here is an intuitive explanation of why quicksort runs in $O(n\log n)$ time in the average case.

How likely is it that a randomly selected pivot is a good one? The best possible selection for the pivot would be the median key, because exactly half of elements would end up left, and half the elements right, of the pivot. However, we have only a probability of $1/n$ that a randomly selected pivot is the median, which is quite small.

Suppose we say a key is a good enough pivot if it lies in the center half of the sorted space of keys – those ranked from $n/4$ to $3n/4$ in the space of all keys to be sorted. Such good enough pivot elements are quite plentiful, since half the elements lie closer to the middle than to one of the two ends, so we have a probability of $1/2$ of picking one. We will make good progress towards sorting whenever we pick a good enough pivot.

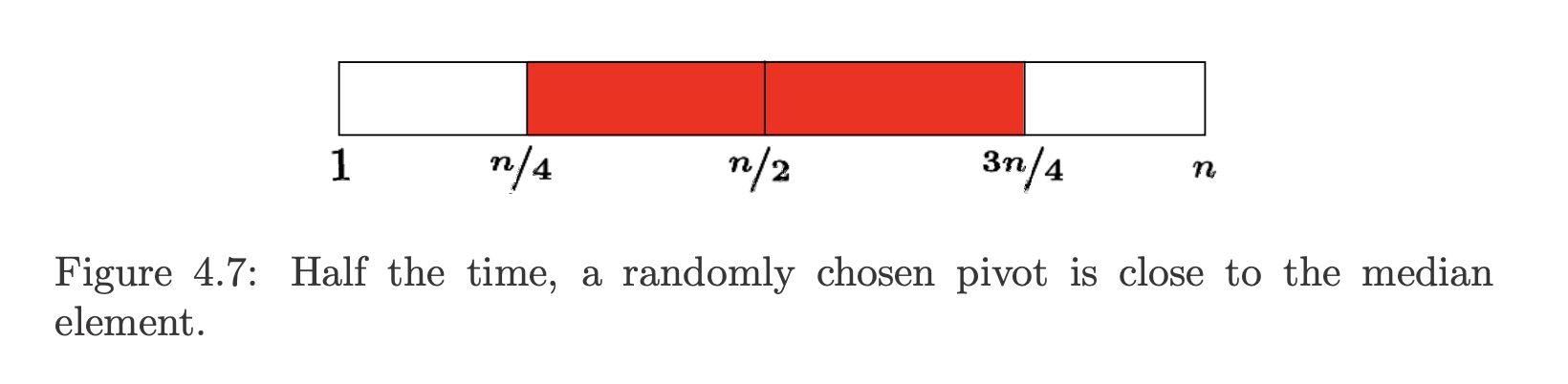
The worst possibly good enough pivot leaves the bigger of the two partitions with $3n/4$ items. This is also the expected size (idea of expected value) of the larger partition left after picking a random pivot $p$, at the median between the worse possible pivot ($p=1$ or $p=n$ leaving a partition of size $n-1$), and the best possible pivot ($p=n/2$ leaving two partitions of size $n/2$).

So what is the height $h_g$ of a quicksort partition tree constructed repeatedly from the expected pivot value? The deepest path through this tree passes through partitions of size $n,(3/4)n,(3/4{)}^{2}n,\dots ,$ down to $1$. How many times can we multiply $n$ by $3/4$ until it gets down to $1$?

$$(3/4{)}^{h_g}n=1⟶n={\left(\frac{4}{3}\right)}^{h_g}$$

so $h_g={\log }_{4/3}n$.

• On average, random quicksort partition trees (and by analogy, binary search trees under random insertion) are very good. More careful analysis shows the average height after $n$ insertions is approximately $2\ln n$. Since $2\ln n\approx 1.386\lg n$, this is only 39% taller than a perfectly balanced binary tree.
• Since quicksort does $O(n)$ work partitioning on each level, the average time is $O(n\log n)$.
• If we are extremely unlucky, and our randomly selected elements are always among the largest or smallest element in the array, quicksort turns into selection sort and runs in $O(n^2)$, but the odds against this are vanishingly small.

Randomization

Our quicksort implementation selected the last element in each sub-array as a pivot. If this program were given a sorted array as input, then at each step it would pick the worst possible pivot, and run in quadratic time.

For any deterministic method of pivot selection, there exists a worst-case input instance which will doom us to quadratic time. We can only claim that quicksort runs in $\Theta (n\log n)$ time, with high probability, if we give it randomly ordered data to sort.

But what if we add an initial step where we randomly permute the order of $n$ elements before we try to solve them. This can be done in $O(n)$ time (see random number generation). This seems like a lot of work but provides the guarantee that we can expect $\Theta (n\log n)$ running time whatever the initial input was. The worst case performance still can happen, but it now depends only upon how unlucky we are. Now, we can claim that randomized quicksort runs in $\Theta (n\log n)$ time on any input, with high probability.

Alternatively, we can get the same guarantee by selecting a random element to be the pivot at each step.