Coordinate Transform for Velocity

Suppose we have a 1-link robot is moving with linear velocity $v$ and angular velocity $\omega$ about $q$:

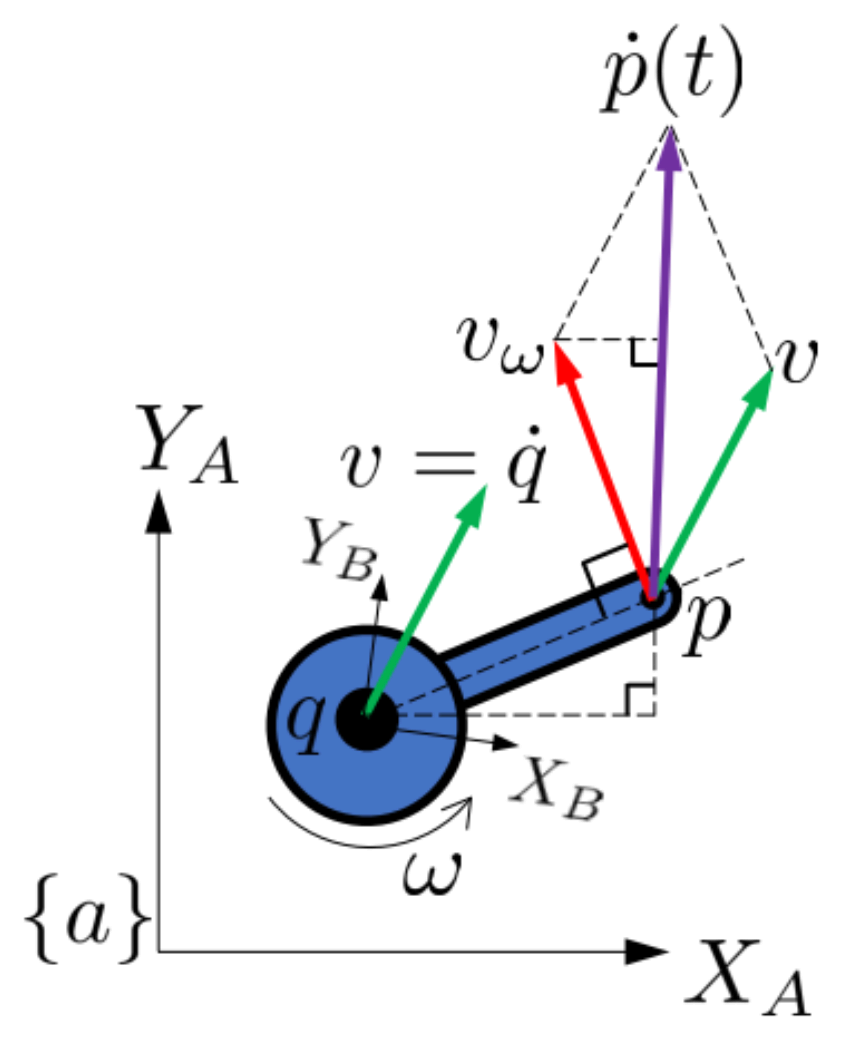
What is ${\dot{p}}^a(t)$, the velocity of $p$ in $\{a\}$?

Velocity due to angular rotation: Note that $||v_w||$, the magnitude of the velocity contribution due to angular velocity, can be written as

$$||v_{\omega }||=\omega ||p^a-q||$$

with similar triangles, we have

$$v_{\omega }=\left[\begin{array}{c}{y}_q-y_p\\ x_p-x_q\end{array}\right]\omega =\left[\begin{array}{cc}0& -\omega \\ \omega & 0\end{array}\right](p^a-q)=:\hat{\omega }(p^a-q)$$

The total velocity ${\dot{p}}^a(t)$ is the summation of two velocity vectors $v$ and $v_w$.

• Note that $v=\dot{q}$ (movement of the base)

$$\begin{array}{rl}{\dot{p}}^a(t)& =v+v_{\omega }\\ & =v+\left[\begin{array}{cc}0& -\omega \\ \omega & 0\end{array}\right](p^a-q)\\ & =v+\hat{\omega }(p^a-q)\\ & =\boxed{\hat{\omega }{p}^a+(v-\hat{\omega }q)}\\ & =\hat{\omega }(R_b^a{p}^b+q)+(v-\hat{\omega }q)\\ & =\hat{\omega }{R}_b^a{p}^b+v\end{array}$$

This is the same idea as rotation + translation, where the first term is the term rotated, and then we add a velocity vector.

Homogeneous Coordinates

To generalize to homogeneous coordinates, consider:

$$\begin{array}{rl}\frac{d}{dt}{\overline{p}}^a(t)& =\frac{d}{dt}\left[\begin{array}{c}{p}^a(t)\\ 1\end{array}\right]=\left[\begin{array}{c}{\dot{p}}^a(t)\\ 0\end{array}\right]\\ & =\left[\begin{array}{cc}\hat{\omega }& v-\hat{\omega }q\\ 0& 0\end{array}\right]\left[\begin{array}{c}{p}^a(t)\\ 1\end{array}\right]\\ & =\left[\begin{array}{cc}\hat{\omega }{R}_b^a& v\\ 0& 0\end{array}\right]\left[\begin{array}{c}{p}^b\\ 1\end{array}\right]\end{array}$$

Thus, we have:

$$\begin{array}{rl}{\dot{\overline{p}}}^a(t)& =\left[\begin{array}{c}{\dot{p}}^a(t)\\ 0\end{array}\right]=\left[\begin{array}{cc}\hat{\omega }& v-\hat{\omega }q\\ 0& 0\end{array}\right]\left[\begin{array}{c}{p}^a(t)\\ 1\end{array}\right]\\ & =\left[\begin{array}{cc}\hat{\omega }& \dot{q}-\hat{\omega }q\\ 0& 0\end{array}\right]{\overline{p}}^a(t)\\ & =\left[\begin{array}{cc}\hat{\omega }{R}_b^a& v\\ 0& 0\end{array}\right]{\overline{p}}^b\end{array}$$

Homogeneous Transformation

Recall that a point in frame $\{a\}$ can be expressed in terms of frame $\{b\}$ as:

$${\overline{p}}^a(t)={\mathcal{G}}_b^a(t){\overline{p}}^b$$

Then:

$${\dot{\overline{p}}}^a(t)={\dot{\mathcal{G}}}_b^a(t){\overline{p}}^b$$

where

$${\mathcal{G}}_b^a(t)=\left[\begin{array}{cc}{R}_b^a(t)& q(t)\\ 0& 1\end{array}\right]⟹{\dot{\mathcal{G}}}_b^a=\left[\begin{array}{cc}{\dot{R}}_b^a(t)& \dot{q}(t)\\ 0& 0\end{array}\right]$$

• ${\dot{R}}_b^a(t)=\hat{\omega }{R}_b^a$ (see time derivative of rotation matrix)
• $\dot{q}(t)=v$

Since we can write ${\overline{p}}^b=({\mathcal{G}}_b^a(t){)}^{-1}{\overline{p}}^a(t)$, we can write

$${\dot{\overline{p}}}^a(t)={\dot{\mathcal{G}}}_b^a(t){\overline{p}}^b={\dot{\mathcal{G}}}_b^a(t)({\mathcal{G}}_b^a(t){)}^{-1}{\overline{p}}^a(t)$$

Let’s consider the ${\dot{\mathcal{G}}}_b^a(t)({\mathcal{G}}_b^a(t){)}^{-1}$ term. This is called the twist matrix:

$$\begin{array}{rl}\hat{\xi }=\dot{\mathcal{G}}{\mathcal{G}}^{-1}& =\left[\begin{array}{cc}\dot{R}& \dot{q}\\ 0& 0\end{array}\right]\left[\begin{array}{cc}{R}^T& -R^{T}q\\ 0& 1\end{array}\right]\\ & =\left[\begin{array}{cc}\dot{R}{R}^T& \dot{q}-\dot{R}{R}^{T}q\\ 0& 0\end{array}\right]\\ & =\left[\begin{array}{cc}\hat{\omega }& \dot{q}-\hat{\omega }q\\ 0& 0\end{array}\right]\\ & =\left[\begin{array}{cc}\hat{\omega }& \kappa \\ 0& 0\end{array}\right]\end{array}$$

We can represent this as a simple vector (twisted) as

$$\xi =\left[\begin{array}{c}\kappa \\ \omega \end{array}\right]\in {\mathbb{R}}^3$$

• $\kappa =\dot{q}-\hat{\omega }q\in {\mathbb{R}}^2$ that encodes the translational velocity contribution.

The instantaneous center of rotation is given by $-{\hat{\omega }}^{-1}$.