Coordinate Transformation in 2D

When thinking about robotics, we typically want to consider the following standard coordinate frames:

• Global (spatial, fixed) frame: A fixed frame of reference attached to the earth.
• Local (body, moving) frame: A frame placed in some key locations within the robot.

Coordinate transformations are a mathematical relation between a point seem from one frame, with the same point seen from another frame. Essentially, they tell us the position and orientation of a coordinate frame with respect to another frame.

Rotation in 2D

Assuming only rotation (no translation yet) between our global and local frames for now, how do transform a point $p^b=(x^b,y^b)$ to $p_a=(x^a,y^a)$?

We can do this using a Rotation Matrix:

$$\begin{array}{rl}{p}_a=\left[\begin{array}{c}{x}^b\\ y^b\end{array}\right]& =\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{x}^b\\ y^b\end{array}\right]\\ & =R_b^a{p}^b\end{array}$$

where $R_b^a$ is a rotation matrix that transforms a vector from frame $b$ into frame $a$.

For a nice visual derivation on the matrix, see here. (Note that the derived matrix here is the inverse of what we wrote above, but this is fine because it’s just going in the other direction.)

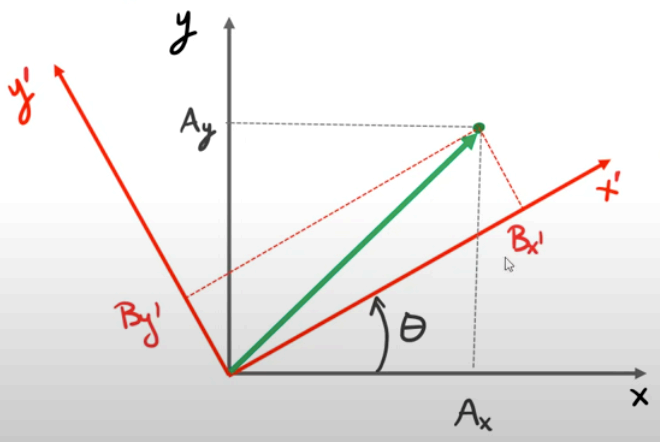
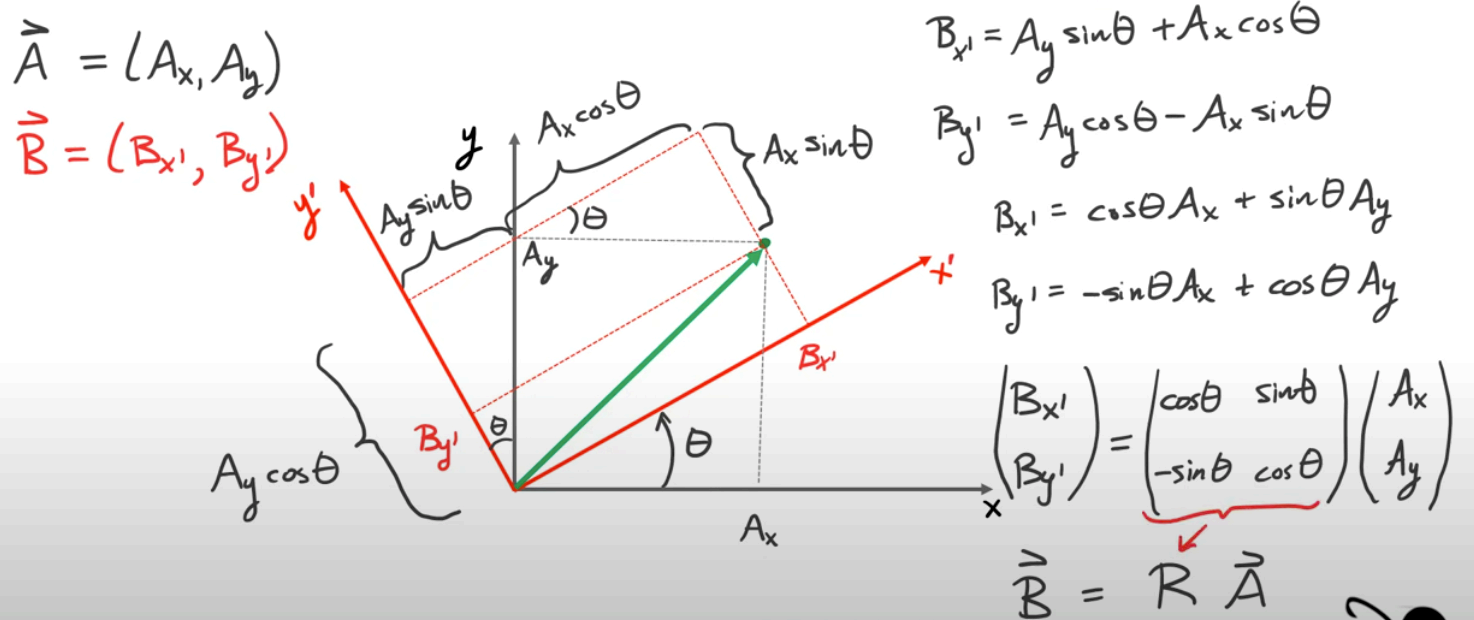
The rotation matrix has some special properties:

• Its inverse is equal to its transpose:

$$(R_b^a{)}^{-1}=(R_b^a{)}^T$$

• Its inverse is also equal to a rotation matrix that goes the other way (from frame $a$ to frame $b$):

$$(R_b^a{)}^T=R_a^b$$

• Multiplying it by its transpose give the identity matrix (orthogonal matrix):

$$R{R}^T=R^{T}R=I$$

We say that $R\in SO(2)$ which stands for Special Orthogonal Group in 2D.

Time derivative of rotation matrix

If the angle $\theta$ changes with time, then we can take the time derivative of the rotation matrix:

$$\dot{R}=\left[\begin{array}{cc}-\sin \theta & -\cos \theta \\ \cos \theta & -\sin \theta \end{array}\right]\dot{\theta }$$

Recall that $\dot{\theta }=\omega$ is the angular velocity.

We can factor the above derivative into a nice form:

$$\begin{array}{rl}\dot{R}& =\left[\begin{array}{cc}0& -\omega \\ \omega & 0\end{array}\right]R\\ & =\hat{\omega }R\end{array}$$

This is the matrix representation of angular velocity in 2D. Note that we can also write

$$\dot{R}{R}^T=\left[\begin{array}{cc}-\sin \theta & -\cos \theta \\ \cos \theta & -\sin \theta \end{array}\right]\omega \left[\begin{array}{cc}\cos \theta & \sin \theta \\ -\sin \theta & \cos \theta \end{array}\right]=\omega$$

Note that this matrix is skew-symmetric such that ${\hat{\omega }}^T=-\hat{\omega }$.

For a point $p^a$, we can find its time derivative using the above as

$${\dot{p}}^a={\dot{R}}_b^a{p}^b=\hat{\omega }{R}_b^a{p}^b$$

Alternatively, we can write

$${\dot{p}}^a={\dot{R}}_b^a(R_b^a{)}^T{p}^a=\hat{\omega }{p}^a$$

Rotation + Translation in 2D

What if we rotate but also have a translation between the coordinate frames? How do transform a point $p^b=(x^b,y^b)$ to $p_a=(x^a,y^a)$?

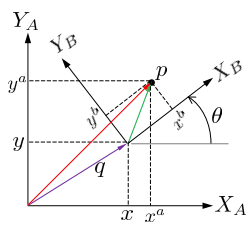
This can be done in two steps.

First, we rotate frame $b$ by $\theta$ using the rotation matrix:

$$\begin{array}{r}\left[\begin{array}{c}{x}^b\\ y^b\end{array}\right]⟶\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]\left[\begin{array}{c}{x}^b\\ y^b\end{array}\right]=R_b^a{p}^b\end{array}$$

Then, we translate $R_b^a{p}^b$ by $q$:

$$R_b^a{p}^b⟶R_b^a{p}^b+q$$

Thus, $p^a=R_b^a{p}^b+q$. Note that this means $q$ is in frame $a$.

Homogeneous Representation

We can represent this rotation + translation as one matrix using Homogeneous Coordinates.

Let

$$\begin{array}{rl}{\mathcal{G}}_b^a& =\left[\begin{array}{cc}{R}_b^a& q\\ 0& 1\end{array}\right]\in {\mathbb{R}}^{3\times 3}\\ {\overline{p}}^a& :=\left[\begin{array}{c}{p}^a\\ 1\end{array}\right],{\overline{p}}^b:=\left[\begin{array}{c}{p}^b\\ 1\end{array}\right]\in {\mathbb{R}}^3\end{array}$$

Then, we write the rotation + translation as

$${\overline{p}}^a={\mathcal{G}}_b^a{\overline{p}}^b$$

We denote ${\mathcal{G}}_b^a\in \text{SE}(2)$ which is the Special Euclidean Group for 2D.

Properties

Composition:

$${\mathcal{G}}_b^a{\mathcal{G}}_c^b={\mathcal{G}}_c^a⟹{\mathcal{G}}_b^a{\mathcal{G}}_c^b{\overline{p}}^c={\mathcal{G}}_b^a{\overline{p}}^b={\overline{p}}^a$$

Inverse:

$$\begin{array}{rl}{\mathcal{G}}_b^a& =\left[\begin{array}{cc}{R}_b^a& q\\ 0& 1\end{array}\right]\\ {\mathcal{G}}_b^a& =({\mathcal{G}}_a^b{)}^{-1}=\left[\begin{array}{cc}(R_b^a{)}^{-1}& -(R_b^a{)}^{-1}q\\ 0& 1\end{array}\right]\\ {\mathcal{G}}_a^c& =({\mathcal{G}}_c^a{)}^{-1}=({\mathcal{G}}_b^a{\mathcal{G}}_c^b{)}^{-1}=({\mathcal{G}}_c^b{)}^{-1}({\mathcal{G}}_b^a{)}^{-1}={\mathcal{G}}_b^c{\mathcal{G}}_a^b\end{array}$$

$\text{SE}(2)$ can be generalized to $\text{SE}(3)$ in the same way with $3\times 3$ rotation matrices.

• 3D rotation matrices are tricky to handle, so we often use other parameterizations such as Euler Angles, quaternions, etc.

Example

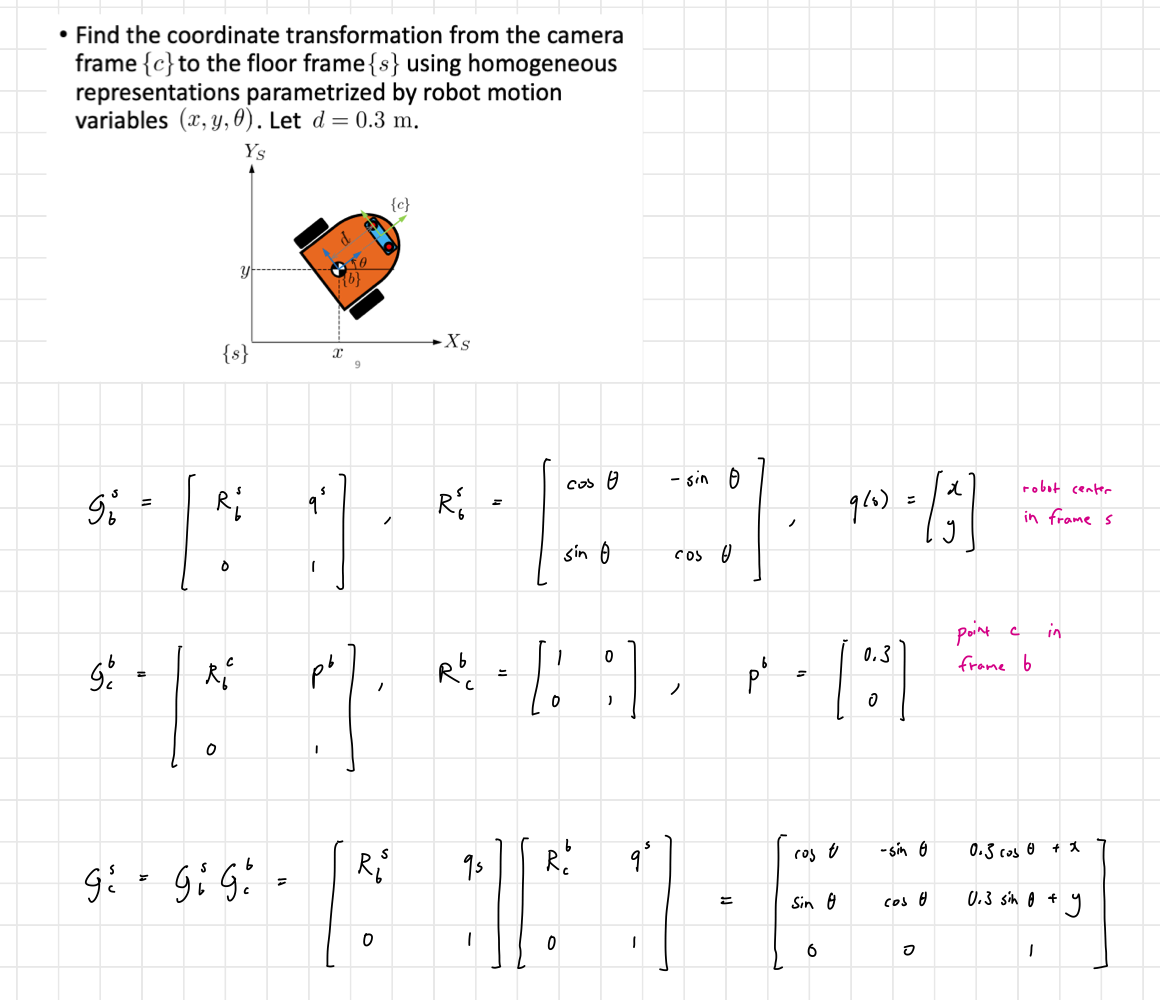
• If an object seen from the camera is located at $(1,1)$ w.r.t to the $c$ frame, then we can find its location in $s$ frame using ${\mathcal{G}}_c^s$.