Proportional-Derivative Control

We saw that simply using proportional feedback affected the coefficient of the constant $s^0$ term, and using derivative feedback affected the coefficient of $s$. What if we combine them?

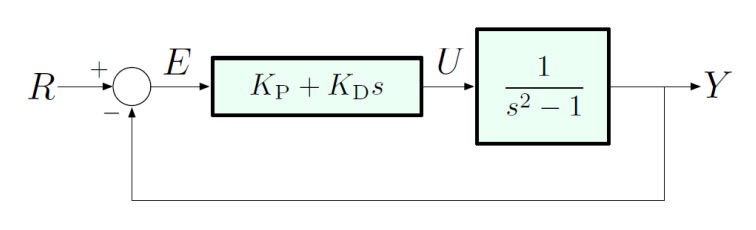
The transfer function is:

$$\frac{Y}{R}=\frac{\frac{K_P+K_{D}s}{s^2-1}}{1+\frac{K_P+K_{D}s}{s^2-1}}=\frac{K_P+K_{D}s}{s^2+K_{D}s+K_P-1}$$

Now, if we set $K_D>0$ and $K_P>1$, then the transfer function will be stable. Furthermore, by choosing $K_P$ and $K_D$, we can arbitrarily assign coefficients of the denominator, therefore the poles of the transfer function. Thus, PD control gives us arbitrary pole placement.

Also note that the addition of the P-gain moves the zero (solution to numerator term):

$$K_{D}s+K_P=0$$

where the LHP zero at $-\frac{K_P}{K_D}$.

But what’s missing?

$$\begin{array}{rl}\text{DC gain}& =\frac{Y}{R}{|}_{s=0}\\ & =\frac{K_P}{K_P-1}\\ & \ne 1\end{array}$$

Thus, with PD control, we can’t have perfect tracking of constant reference.