Feedback System Type

The fact that adding an integrator term to a PD controller leads to perfect tracking of constant references and perfect rejection of constant disturbances is a special case of a more general analysis.

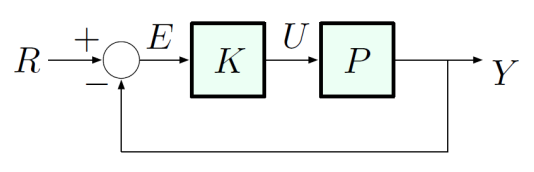
Consider the reference

$$r(t)=\frac{t^k}{k!}1(t)⟷R(s)=\frac{1}{s^{k+1}}$$

• $k=0$ would give us a step (position)
• $k=1$ would give us a ramp (velocity)
• $k=2$ would give us a parabola (acceleration)

The error signal is given by:

$$E=\frac{1}{1+KP}R=\frac{1}{1+KP}\frac{1}{s^{k+1}}$$

The Final Value Theorem (assuming stability) gives

$$e(\infty )=sE(s){|}_{s=0}=\frac{1}{1+KP}\frac{1}{s^k}{|}_{s=0}$$

System Type

The system type is the number $n$ of poles the forward-loop transfer function $KP$ has at the origin ($s=0$). It is the degree of the lowest-degree polynomial that cannot be tracked in feedback with zero steady-state error.

• Note that the system type is calculated from the forward-loop transfer function, although the conclusions drawn are about the closed-loop system.

Let’s suppose that $KP$ has an $n$-th order pole at $s=0$:

$$KP=\frac{K_0}{s^n}$$

Then:

$$sE(s)=\frac{1}{\left(1+\frac{K_0}{s^n}{s}^k\right)}=\frac{s^{n-k}}{s^n+K_0}$$

Recall that the reference $r(t)$ is a polynomial of degree $k$. There are three cases to consider:

• Perfect tracking: $n>k:e(\infty )=0$
• Imperfect tracking: $n=k:e(\infty )=\text{const}\ne 0$ gives imperfect tracking
• No tracking: $n<k:e(\infty )=\infty$

Examples

• Type 0: No pole at origin. This is what we had without the integral gain term: nonzero steady-state error to constant references.
• Type 1: A single pole at the origin. This is what we get with an integral gain term: we can track constant references and reject constant disturbances with zero error. However, we can’t track higher order references like ramp signals.
• Type 2: A double pole at the origin. Can track ramp references without error, but not $t^2,t^3$, etc.