Undamped Response for Second-Order System

Consider the undamped systems shown below. They all have the same model form: $m\ddot{x}+kx=f(t)$. We can consider this to be the same as the general second-order system $m\ddot{x}+c\dot{x}+kx=f(t)$ above but with $c=0$.

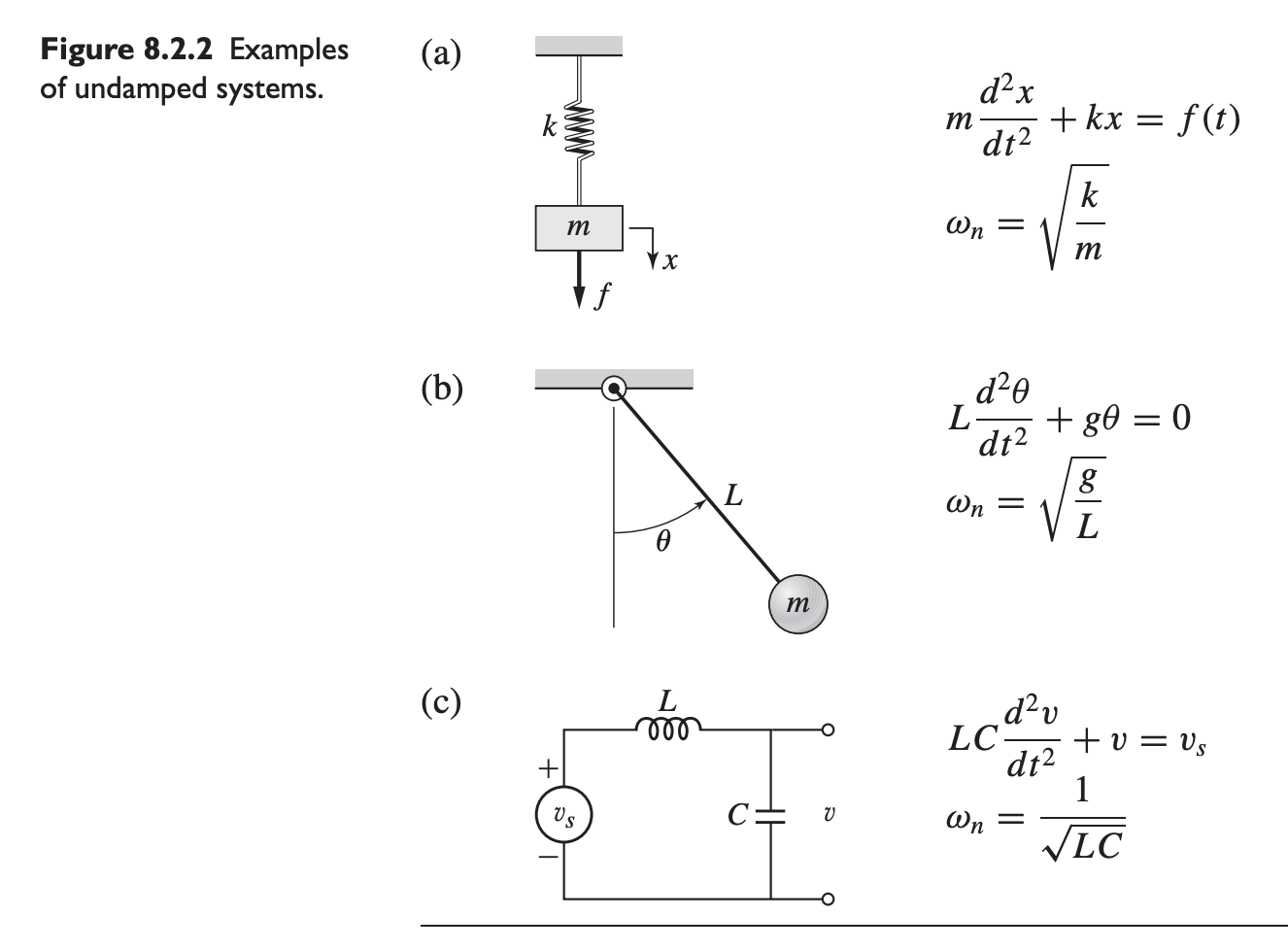
We established that for second-order systems, we have

$$X(s)=\underset{\text{ZSR}}{\underbrace{\frac{F(s)}{m{s}^2+cs+k}}}+\underset{\text{ZIR}}{\underbrace{\frac{msx(0)+m\dot{x}(0)+cx(0)}{m{s}^2+cs+k}}}$$

With $c=0$, this becomes:

$$\begin{array}{rl}X(s)& =\underset{\text{ZSR}}{\underbrace{\frac{F(s)}{m{s}^2+k}}}+\underset{\text{ZIR}}{\underbrace{\frac{msx(0)+m\dot{x}(0)}{m{s}^2+k}}}\\ & =\frac{F(s)/m}{s^2+\frac{k}{m}}+\frac{\dot{x}(0)+sx(0)}{s^2+\frac{k}{m}}\end{array}$$

For the free response (ZIR) case of $F(s)=0$:

$$X(s{)}_{\text{ZIR}}=\frac{\dot{x}(0)}{s^2+\frac{k}{m}}+\frac{sx(0)}{s^2+\frac{k}{m}}$$

And the transfer function is:

$$\frac{X(s)}{F(s)}=\frac{\frac{1}{m}}{s^2+\frac{k}{m}}$$

where $s^2+\frac{k}{m}$ is the characteristic equation.

What if we solve the characteristic equation? We have

$$\begin{array}{rl}{s}^2+\frac{k}{m}& =0\\ s^2& =-\frac{k}{m}\\ s& =\pm j\sqrt{\frac{k}{m}}\\ {\omega }_n& =\sqrt{\frac{k}{m}}\end{array}$$

where ${\omega }_n$ is the natural frequency of the undamped system. Then, we can write:

$$\begin{array}{rl}X(s)& =\frac{\dot{x}(0)}{s^2+\frac{k}{m}}+\frac{sx(0)}{s^2+\frac{k}{m}}\\ & =\frac{\dot{x}(0)}{s^2+{\omega }_n^2}+\frac{sx(0)}{s^2+{\omega }_n^2}\\ & =\frac{\dot{x}(0)}{s^2+{\omega }_n^2}\cdot \frac{{\omega }_n}{{\omega }_n}+\frac{sx(0)}{s^2+{\omega }_n^2}\\ & =\frac{\dot{x}(0)}{{\omega }_n}\cdot \frac{{\omega }_n}{s^2+{\omega }_n^2}+x(0)\frac{s}{s^2+{\omega }_n^2}\end{array}$$

Recall that:

$$\mathcal{L}[\cos (bt)ut]=\frac{s}{s^2+b^2},\mathcal{L}[\sin (bt)ut]=\frac{b}{s^2+b^2}$$

Thus, we have:

$$x(t{)}_{\text{ZIR (Free response)}}=\left[\frac{\dot{x}(0)}{{\omega }_n}\sin ({\omega }_{n}t)+x(0)\cos ({\omega }_{n}t)\right]u(t)$$

This solution shows that the mass oscillates about the rest position $x=0$ with a frequency of ${\omega }_n$. The period of the oscillation is $2\pi /{\omega }_n$.

So we have some shit like

$$m\ddot{x}+c\dot{x}+kx=0$$

We assume that $x=e^{st}$. Then:

$$\begin{array}{rl}\dot{x}& =s{e}^{st}\\ \ddot{x}& =s^2{e}^{st}\end{array}$$

so we have

$$\begin{array}{r}m{s}^2{e}^{st}+cs{e}^{st}+k{e}^{st}=0\\ e^{st}(m{s}^2+cs+k)=0\end{array}$$

So we want to solve $m{s}^2+cs+k$. We have $s$ in the form of

$$s=\sigma +j\omega$$

So we have:

$$e^{st}=e^{(\sigma +j\omega )t}=e^{\sigma t}{e}^{j\omega t}$$

The real part $e^{\sigma t}$ governs the amplitude so if $\sigma >1$ the function explodes, if $\sigma <1$ it’s stable. And this is why the time constant $\tau =\frac{1}{|\sigma |}$ because this tells us how it decays.

The imaginary one is a sinusoid like

$$e^{j\omega t}=\cos (\omega t)+j\sin (\omega t)$$

Given:

$$s=\sigma +j\omega$$

We have:

$$\begin{array}{rl}{\omega }_d& =\omega \\ {\omega }_n& =\sqrt{{\sigma }^2+{\omega }^2}\\ \tau & =\frac{1}{|\sigma |}\\ \zeta & =\frac{\sigma }{{\omega }_n}=\cos \left({\tan }^{-1}\left(\frac{\omega }{\sigma }\right)\right)\end{array}$$

• If $\sigma >1$, the system is unstable (increases over time) so $\zeta$ and $\tau$ are undefined.
• If the roots are real and equal, (eg. $s=-10,-10$ or something), ${\omega }_d$ and ${\omega }_n$ are not defined because there’s no oscillation.
• If there is only one root, the system is first order, so damping $\zeta$ is not defined, and ${\omega }_d$ and ${\omega }_n$ are not defined because there’s no oscillation.