Time Domain Response of Second-Order Systems

See specific response types:

• Undamped Response for Second-Order System
• Damped Response for Second-Order System

General Second-Order Systems

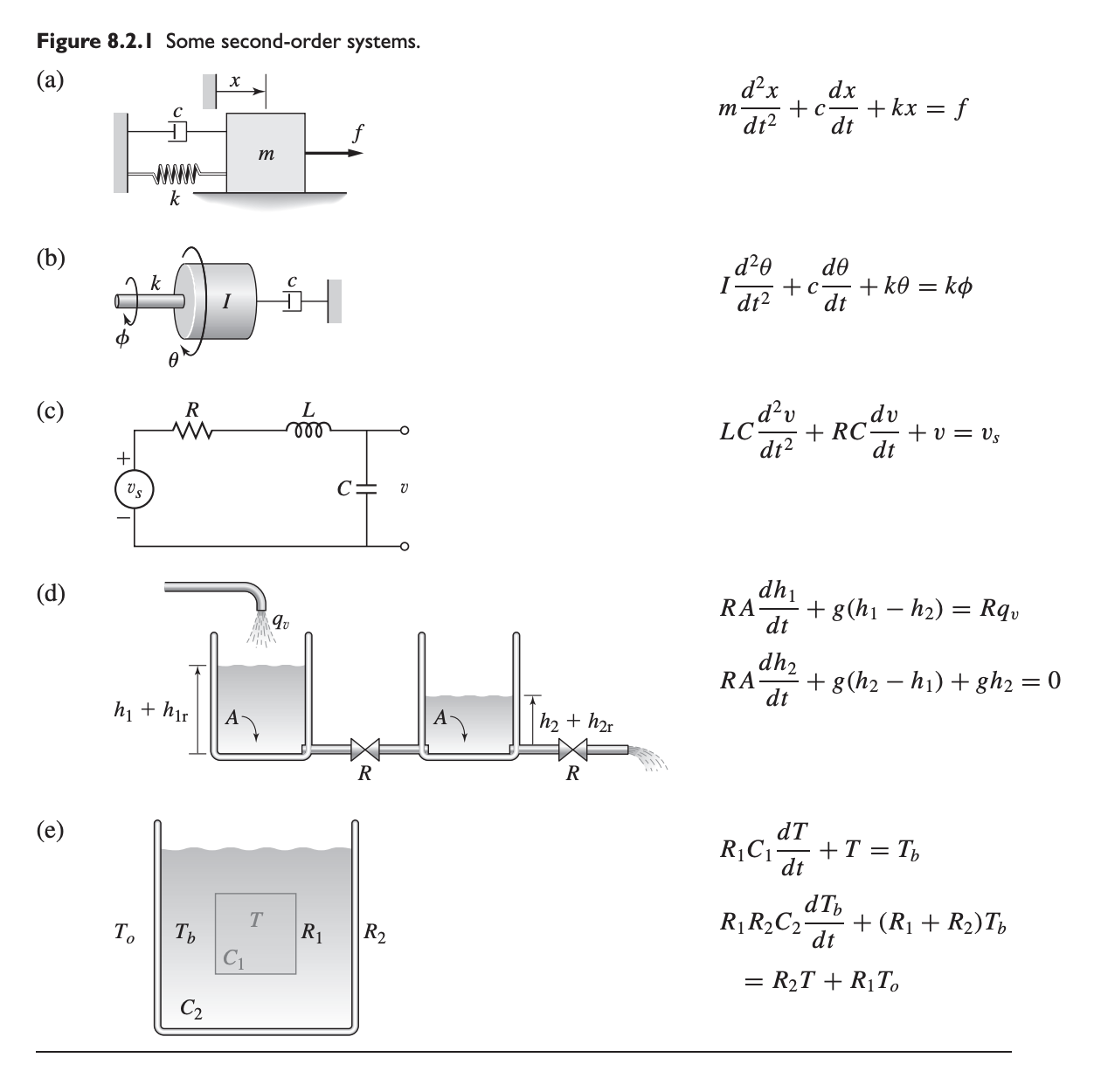
The equations of motion of many systems containing mass, spring, and damping elements have the form:

$$m\ddot{x}+c\dot{x}+kx=f(t)$$

where $f(t)$ is the input. The Laplace transform of this is:

$$m[s^{2}X(s)-sx(0)-\dot{x}(0)]+c[sX(s)-x(0)]+kX(s)=F(s)$$

Re-arranging:

$$(m{s}^2+cs+k)X(s)=F(s)+msx(0)+m\dot{x}(0)+cx(0)$$

Solving for $X(s)$:

$$X(s)=\underset{\text{ZSR}}{\underbrace{\frac{F(s)}{m{s}^2+cs+k}}}+\underset{\text{ZIR}}{\underbrace{\frac{msx(0)+m\dot{x}(0)+cx(0)}{m{s}^2+cs+k}}}$$

The transfer function is then:

$$\frac{X(s)}{F(s)}=\frac{1}{m{s}^2+cs+k}$$

The solution of the system $m\dot{x}+c\dot{x}+kx=f(t)$, and therefore the form of the free and forced responses, depends on the values of the two characteristic roots, obtained from the characteristic equation $m{s}^2+cs+k=0$.

Numerator Dynamics

Another related model has the form

$$m\ddot{x}+c\dot{x}+kx=a\dot{g}(t)+bg(t)$$

This is essentially the same equation as before but we have $f(t)=a\dot{g}(t)+bg(t)$. Taking the Laplace transform, we have:

$$\begin{array}{rl}F(s)& =asG(s)+bG(s)\\ & =(as+b)G(s)\end{array}$$

We still have:

$$\frac{X(s)}{F(s)}=\frac{1}{m^2+cs+k}$$

Its transfer function is:

$$\frac{X(s)}{G(s)}=\frac{as+b}{m{s}^2+cs+k}$$

So this model has numerator dynamics. The input does not affect the characteristic equation, and therefore does not affect the stability of the model or its free response. Thus, this model has the same stability characteristics and the same free response, because they have the same characteristic equation, $m{s}^2+cs+k=0$.