General Planar Motion

General planar motion refers to translation restricted to a plane, and rotation restricted to the axis perpendicular to this plane. A rigid body moves in a plane passing through its center of mass and symmetrical with respect to the plane.

Motion is then described as translation and rotation about an axis perpendicular the the plane.

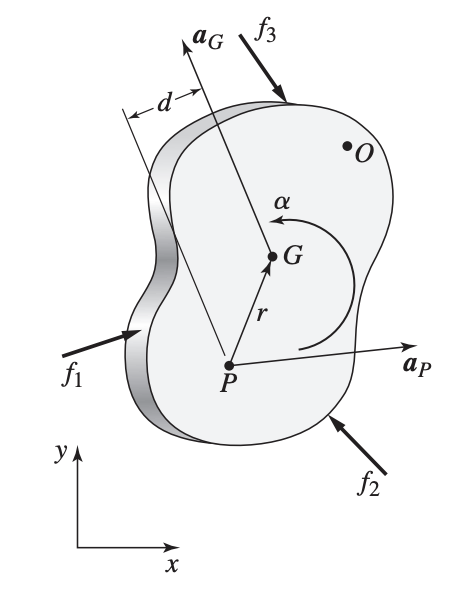
• $G$ is the center of mass
• $O$ is a fixed point (center of rotation)

Force and Moment Equations

We can use two force equations to describe translational motion:

$$\begin{array}{rl}{f}_x& =m{a}_{G_x}\\ f_y& =m{a}_{G_y}\end{array}$$

where $f_x$ and $f_y$ are the net forces acting on the mass $m$ in the $x$ and $y$ directions, respectively. The mass center is located at point $G$. Finally, $a_{G_x}$ and $a_{G_y}$ are the accelerations of the mass center in the $x$ and $y$ directions relative to the fixed $x$-$y$ plane.

When the object is constrained to rotate around an axis $O$, we have

$$I_O\alpha =M_O$$

where $I_O$ is the mass moment of inertia of the body about point $O$, and $M_O$ is the sum of the moments applied to the body about the point $O$.

The equation below applies whether or not the axis of motion is constrained:

$$M_G=I_G\alpha$$

where $M_G$ is the net moment acting on the body about an axis that passes through the mass center $G$ and is perpendicular to the plane of the body. $I_G$ and $\alpha$ are the mass moment of inertia and angular acceleration of the body about this axis.

For an accelerating point $P$, not fixed to the body, we have:

$$\begin{array}{r}{M}_P=M_G+m{a}_{G}d\end{array}$$

where $d$ is the distance between $a_G$ and a parallel line through $P$. (See diagram above!)

Example