Mass Moment of Inertia

$T$ and $\alpha$ are related by $T=I\alpha$ . In this equation, $I$ is the mass moment of inertia (MMI).

• $F=ma$ → $m$ is resistance to acceleration.
• $T=I\alpha$ → $I$ is resistance to angular acceleration.

The mass moment of inertia $I$ about a specified reference axis is defined as:

$$I=\int r^{2}dm$$

where $r$ is the distance from the reference axis to the mass element $dm$.

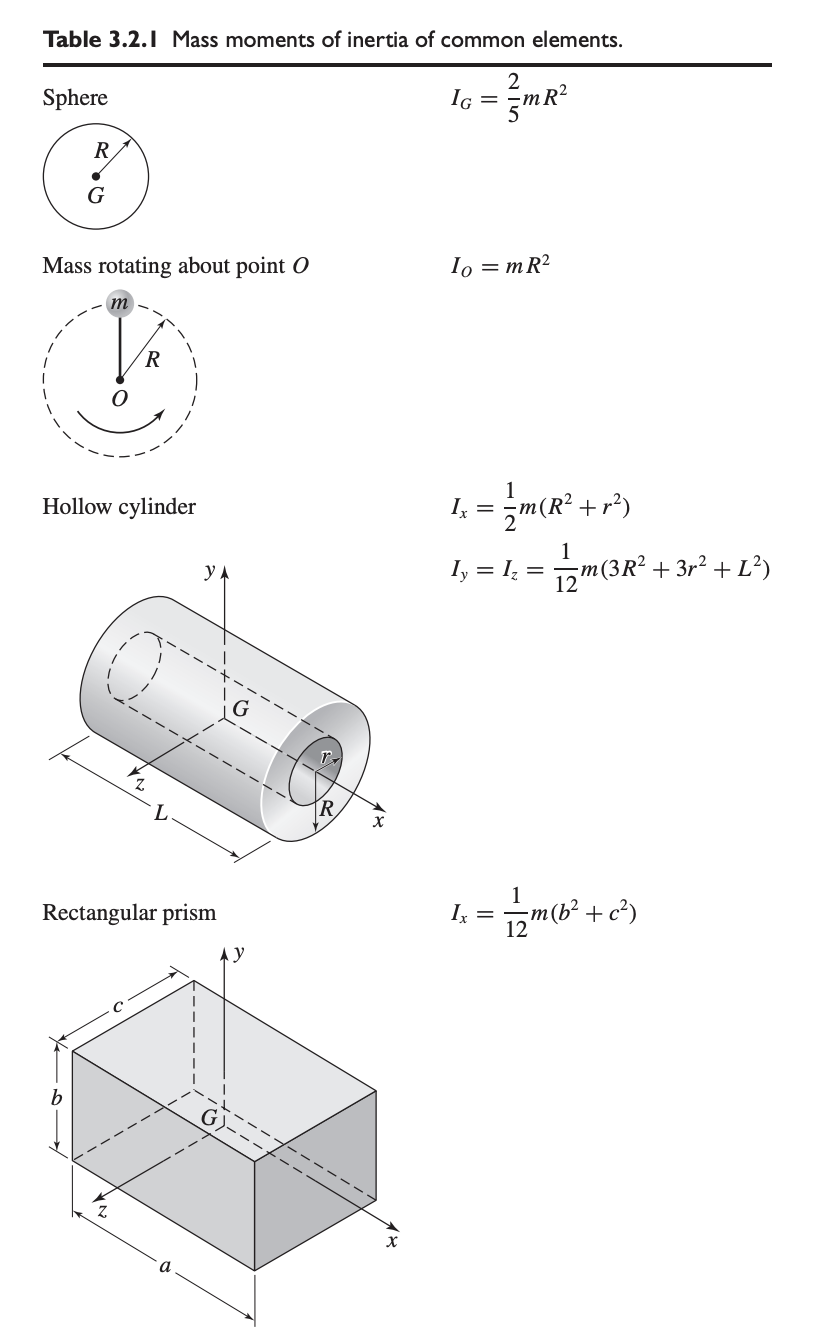
Mass moment of inertia depends on the axis about which the body is rotating. For planar kinetics, rotation is often perpendicular to plane of motion (i.e., rotation about $z$-axis).

Depends on the point of rotation:

• At the mass center ($G$)
• At a fixed point of rotation
• At an arbitrary point that is not $A$ or $B$

For composite bodies, the MMI is determined by algebraically adding together all the mass moments of inertia, found about the same axis, of the different shapes.

Radiation of Gyration

Radius of gyration is a measure of the distribution of the body’s mass about the axis at which the moment of inertia is defined.

$$I=m{k}^2\text{or}k=\sqrt{I/m}$$

Parallel-Axis Theorem

If the rotation axis of a rigid body does not coincide with the body’s axis of symmetry (or mass center), but is parallel to it at a distance $d$, then the mass moment of inertia about the given rotation axis is given by:

$$I=I_s+m{d}^2$$

where $I_s$ is the inertia about the symmetry axis.

Fixed point of rotation:

$$I_O=I_G+m{r}_{G/O}^2$$

Rotation about a point, $A$:

$$I_A=I_G+m{r}_{G/A}^2$$