Transient Heat Transfer

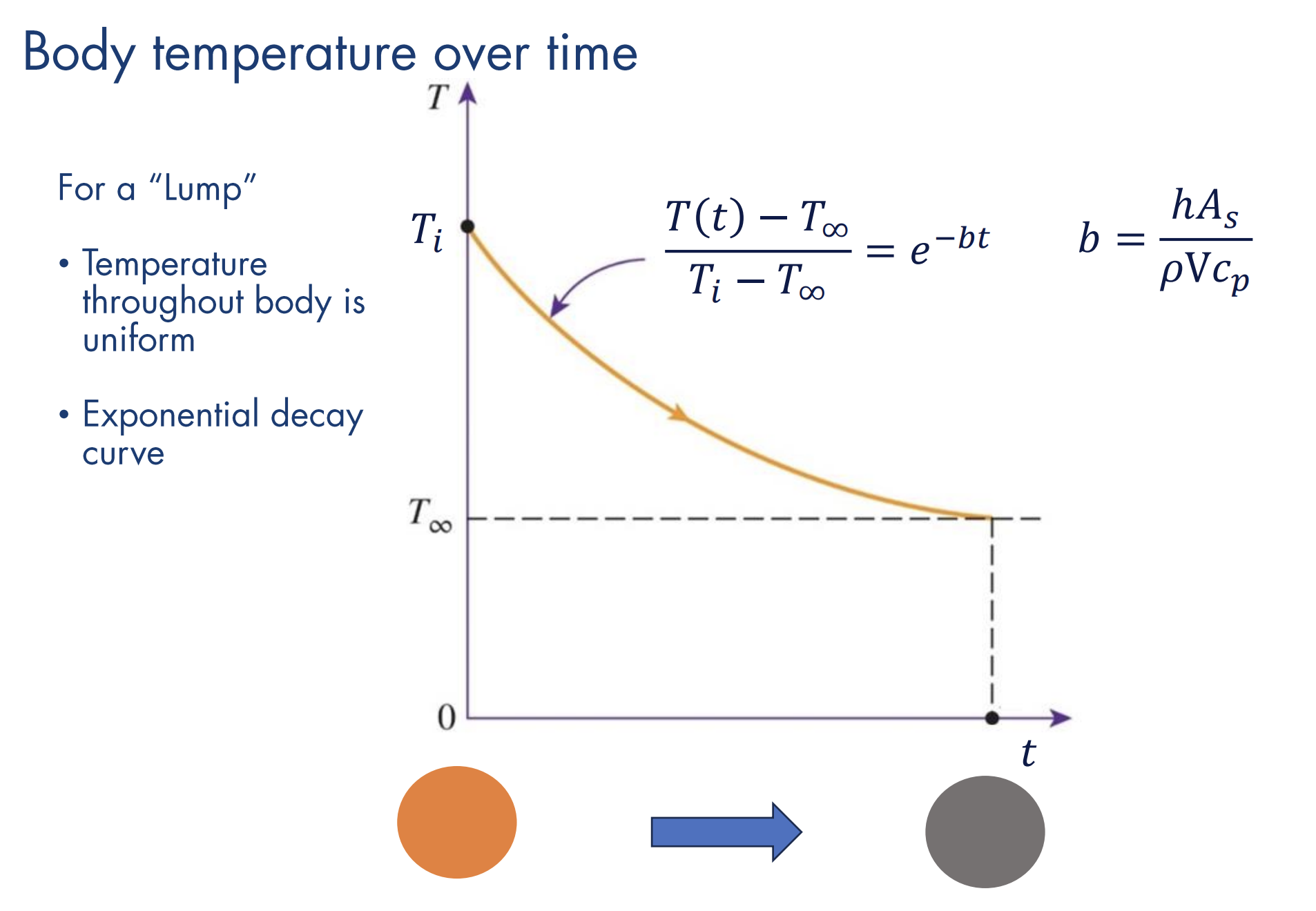
In transient problems, the temperature of a body changes over time, unlike steady-state. To simplify this analysis, it’s useful to treat the body as a lump that has one uniform temperature at a given time.

For the lumped capacitance above, we have:

• Uniform temperature $T$ at each time
• Transient (not steady-state)
• Closed system
• No work, $\dot{W}=0$
• No energy generation
• Constant properties $k,\rho ,c_p$

Then, our energy balance is:

$$\begin{array}{rl}\frac{dE}{dt}& =\dot{Q}-\dot{W}\\ m{c}_p\frac{dT}{dt}& =h{A}_s(T_{\infty }-T(t))\\ \rho V{c}_p\frac{dT}{dt}+h{A}_s(T(t)-T_{\infty })& =0\end{array}$$

Now, let $\theta =T(t)-T_{\infty }$. This gives:

$$\begin{array}{rl}\frac{d\theta }{dt}+\frac{h{A}_s}{pV{c}_p}\theta & =0\\ \frac{d\theta }{dt}+b\theta & =0\end{array}$$

where $b=h{A}_s/pV{c}_p$.

The generation solution to this in the form $\theta =C_1{e}^{-bt}$. The boundary condition we apply to solve this is

$${\theta }_0=T_0-T_{\infty }\text{ at }t=0$$

which gives:

$$\begin{array}{rl}{C}_1={\theta }_0& \\ \theta ={\theta }_0& e^{-bt}\end{array}$$

Then, we have:

$$\boxed{\begin{array}{rl}\frac{T(t)-T_{\infty }}{T_0-T_{\infty }}& =e^{-bt}\text{ where }b=\frac{h{A}_s}{pV{c}_p}=\frac{1}{\tau }\\ & =e^{-t/\tau }\end{array}}$$

where $\tau$ is a time constant.

Thus, this lumped capacitance model gives exponential decay in body temperature.

Criteria for Lumped Capacitance Method

For the lumped capacitance method above to be valid, thermal diffusion (conductivity within the ball) must be much faster than convection outside the ball. This can be characterized by the Biot number:

$$\begin{array}{rl}\text{Bi}& =\frac{\text{Conduction resistance within body}}{\text{Convection resistance at surface of body}}\ll 1\\ \text{Bi}& =\frac{L/k{A}_s}{1/h{A}_s}=\frac{hL}{k}\ll 1\end{array}$$

In general, we want:

$$\text{Bi}=\frac{h{L}_c}{k}\le 0.1$$

where $L_c=\frac{V}{A_s}$ is the characteristic length. For various shapes:

$$\begin{array}{rl}\text{Sphere:}& L_c=\frac{\frac{4}{3}\pi r^3}{4\pi r^2}=\frac{r}{3}\\ \text{Cylinder:}& L_c=\frac{r}{2}\\ \text{Wall:}& L_c=\frac{t}{2}\end{array}$$

Examples

Example 1

First, we want to check that $\text{Bi}\le 0.1$:

$$\begin{array}{rl}{\text{Bi}}_{\text{sphere}}=\frac{h{L}_c}{k}& =\frac{h}{k}\left(\frac{r}{3}\right)\\ & =\frac{(1000[\text{W/}{\text{m}}^2\text{K}])(0.001[\text{m}])}{3(50[\text{W/}\text{mK}])}\\ & =0.066\le 0.1\end{array}$$

Thus, lumped capacitance method is valid.

We have:

$$\begin{array}{rl}\frac{T(t)-T_{\infty }}{(T_0-T_{\infty })}& =\exp \left(-\frac{h{A}_s}{pV{c}_p}t\right)\\ \frac{100-25°\text{C}}{1200-25°\text{C}}& =\exp \left(\frac{-1000\left[\frac{\text{J}}{\text{s}{\text{m}}^2\text{K}}\right]3t}{8000[\text{kg/}{\text{m}}^3](0.01[\text{m}])(502[\text{J/}\text{kg/}\text{K}])}\right)\\ 0.0638& =\exp (-7.47[{\text{s}}^{-1}]t)\\ t& =\frac{\ln (0.0638)}{-7.47[{\text{s}}^{-1}]}\\ & =0.368\text{ s}\end{array}$$

Example 2

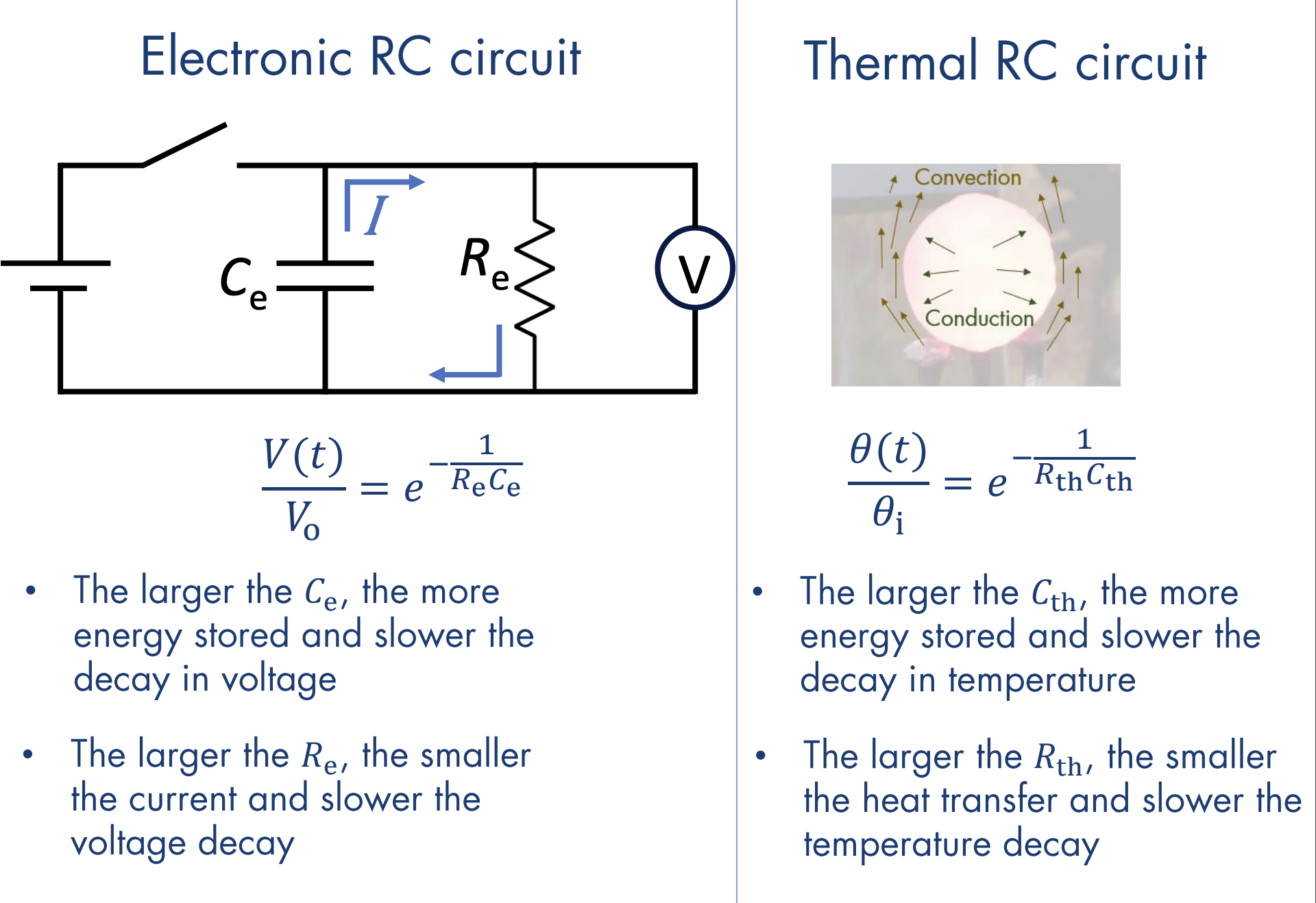
Lumped Capacitance as a Thermal Circuit

Lumped capacitances are similar to RC circuits. We have:

$$\frac{\theta (t)}{{\theta }_0}=e^{-t/\tau }$$

where

$$\tau =\left(\frac{1}{h{A}_s}\right)(pV{c}_p)=R_{\text{th}}{C}_{\text{th}}$$

where $R_{th}$ is the convection resistance and $C_{\text{th}}$ is the thermal capacitance. Convection resistance is used because the object has high thermal conductivity, so heat transfer is limited by the rate at which heat can be transferred to or from the surrounding fluid, which is a convection process.