Thermal Resistance

Conduction Resistance

We showed that steady heat conduction in plane walls can be written as:

$${\dot{Q}}_{\text{cond}}=-kA\frac{dT}{dx}=-kA\left(\frac{T_2-T_1}{L}\right)$$

We can re-write this as:

$$\begin{array}{rl}{\dot{Q}}_{\text{cond, wall}}& =kA\frac{T_1-T_2}{L}\\ & =\frac{T_1-T_2}{R_{\text{wall}}}\end{array}$$

where we have

$$R_{\text{wall}}=\frac{L}{kA}$$

which we call the thermal resistance or conduction resistance of the wall.

More in general, the thermal resistance can be described as the ratio between the driving potential to the corresponding heat transfer rate, $R=\Delta T/{\dot{Q}}_{\text{cond}}$.

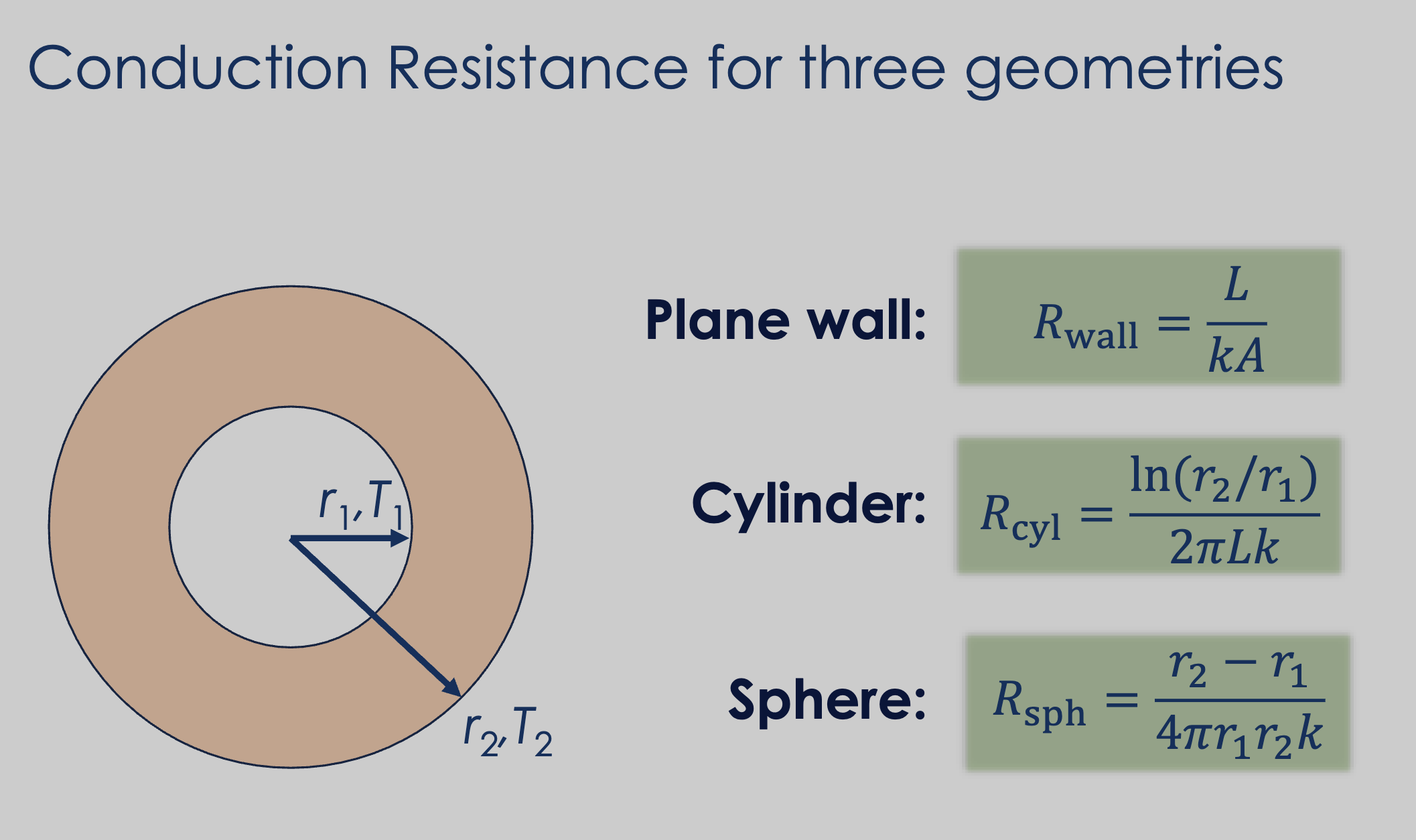
Some other geometries other than plane walls:

Convection Resistance

Consider convection heat transfer from a solid surface of area $A_s$ and temperature $T_s$ to a fluid whose temperature sufficiently far from the surface is $T_{\infty }$, with a convection heat transfer coefficient $h$. Newton’s law of cooling for convection heat transfer rate ${\dot{Q}}_{\text{conv}}=h{A}_s(T_s-T_{\infty })$ can be rearranged as

$${\dot{Q}}_{\text{conv}}=\frac{T_s-T_{\infty }}{R_{\text{conv}}}$$

where \

$$R_{\text{conv}}=\frac{1}{h{A}_s}$$

is the thermal resistance of the surface against heat convection or the convection resistance.

Radiation Resistance

When the wall is surrounded by a gas, the radiation effects, can be significant and may need to be considered. The rate of radiation heat transfer between a surface of emissivity $ϵ$ and area $A_s$ at temperature $T_s$ and the surrounding surfaces at some average temperature $T_{\text{surr}}$ can be expressed as:

$${\dot{Q}}_{\text{rad}}=ϵ\sigma A_s(T_s^4-T_{\text{surr}}^4)=h_{\text{rad}}{A}_s(T_s-T_{\text{surr}})=\frac{T_s-T_{\text{surr}}}{R_{\text{rad}}}$$

where

$$R_{\text{rad}}=\frac{1}{h_{\text{rad}}{A}_s}$$

is the thermal resistance of a surface against radiation, or the radiation resistance.

Electrical Analogy

The above concept of heat transfer with thermal resistance is analogous to electric current flow:

$$I=\frac{V_1-V_2}{R_e}=\sigma A\frac{(V_1-V_2)}{L}$$

where:

$$R_e=\frac{L}{\sigma A}$$

This is very similar to $kA\frac{T_1-T_2}{L}$.

Thermal Resistances in Series and Parallel

Like electrical resistors, thermal resistances in series add together.

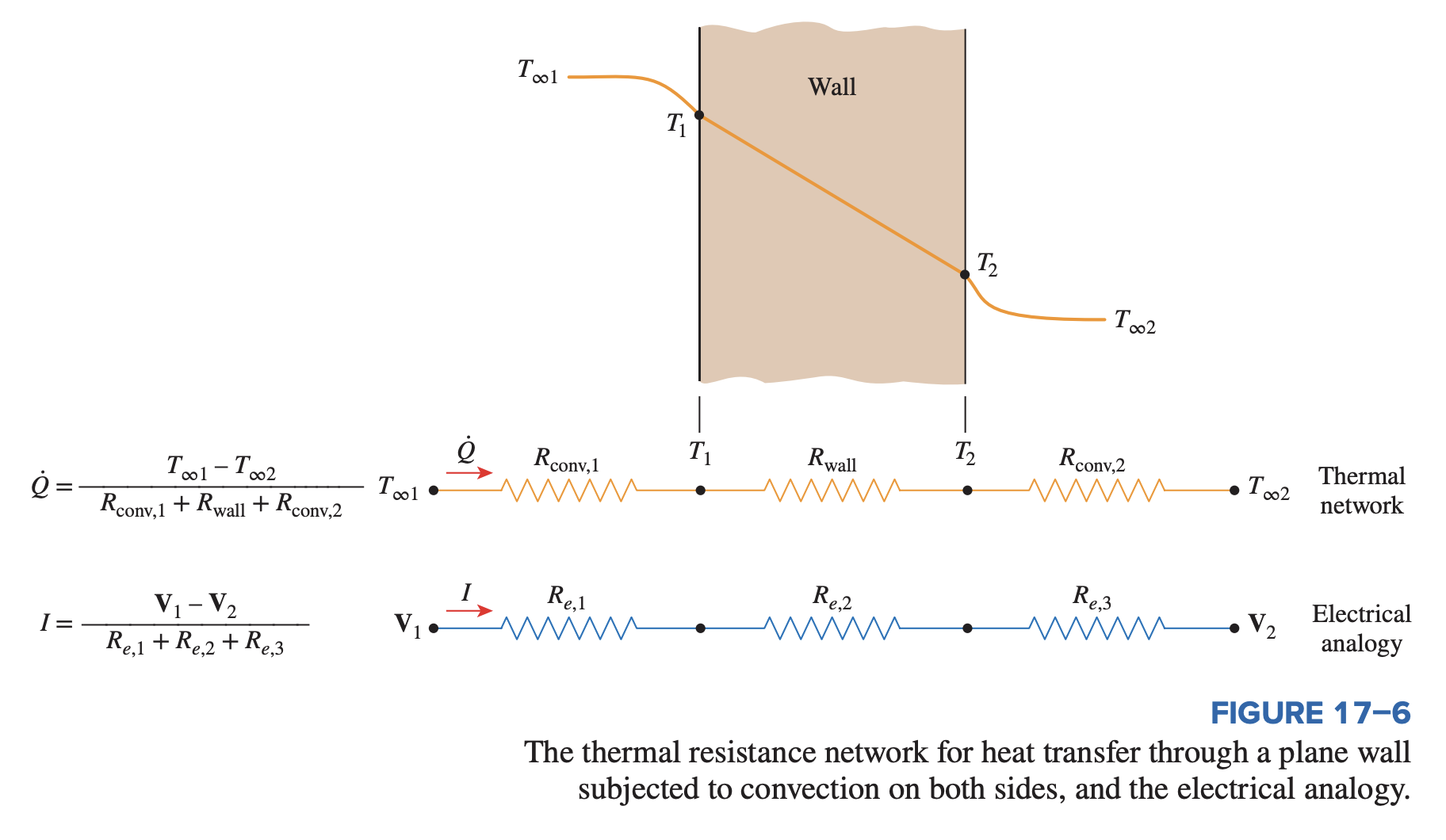
Like electrical resistors, thermal resistances in parallel follow:

$$\frac{1}{R_{eq}}=\frac{1}{R_1}+\frac{1}{R_2}$$

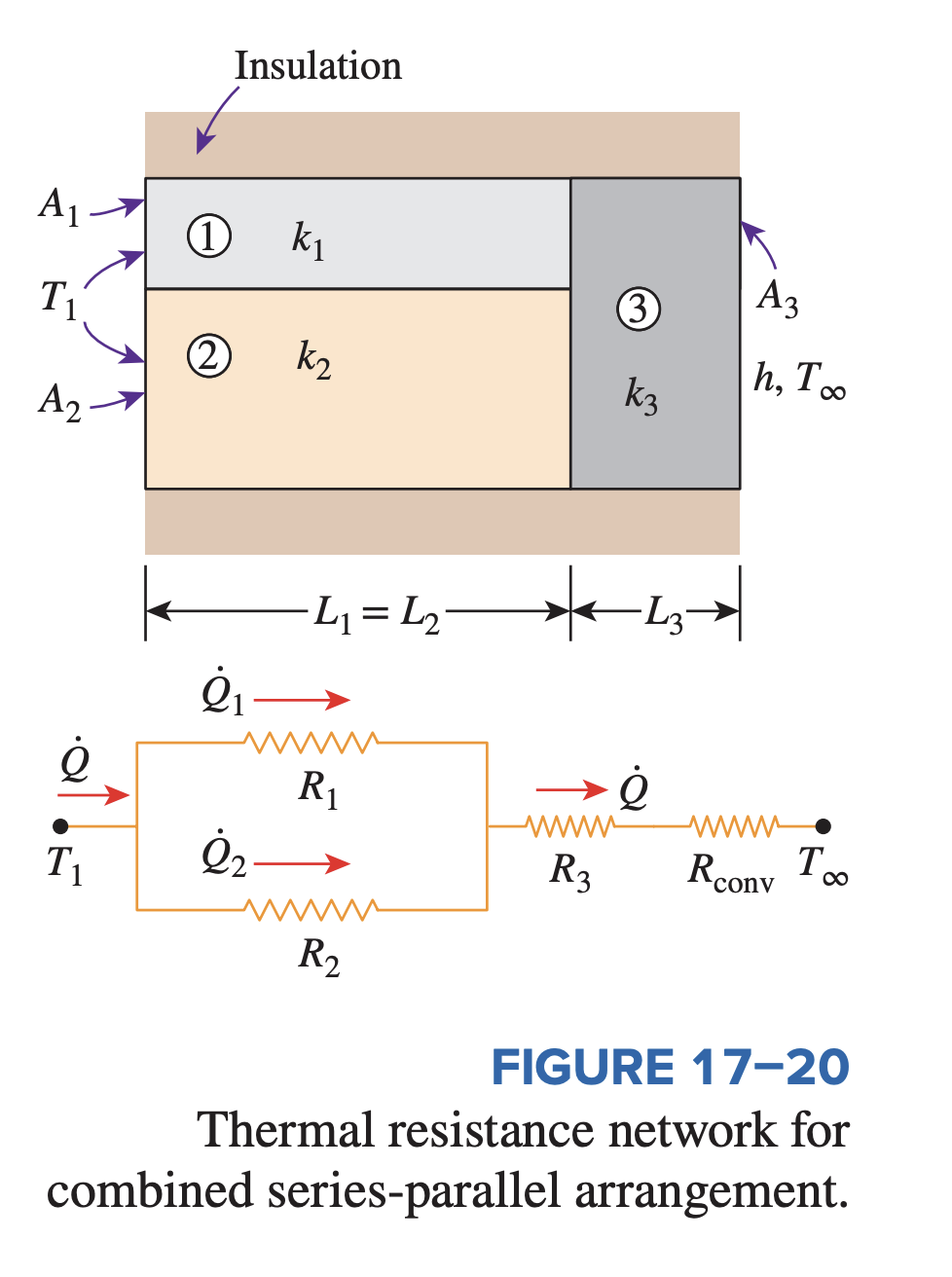
In the case shown above, we would have:

$$R_{\text{total}}=\frac{R_1{R}_2}{R_1+R_2}+R_3+R_{\text{conv}}$$

In general:

• Any plane wall normal to the x-axis is isothermal (the temperature varies in the $x$-direction only)
• Any plane parallel to the x-axis is adiabatic (heat transfer occurs in $x$-axis only)