Finned Surfaces

Recall that:

$${\dot{Q}}_{\text{conv}}=\bar{h}A(T_s-T_{\infty })$$

At times, we would like to increase the rate of heat transfer, $\dot{Q}$, without increasing $\Delta T$ or $h$. To do this, we increase the surface area by attaching to the surface extended surfaces called fins made of highly conductive materials such as aluminum.

We assume:

• Steady operation with no heat generation in the fin
• Thermal conductivity $k$ of the material remains constant
• Convection heat transfer coefficient $h$ is constant and uniform over the surface of the fin

Fin Equation

Consider a volume element of a fin at location $x$ having a length of $\Delta x$, a cross-section area $A_c$, and a perimeter of $p$.

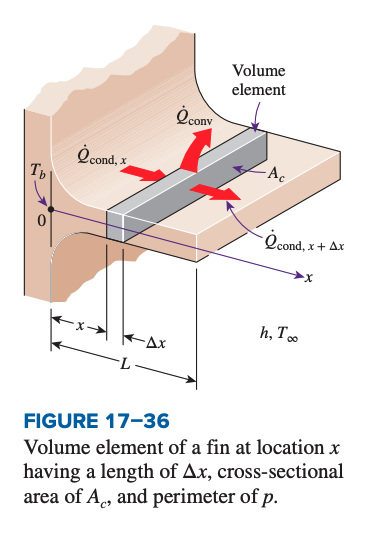
Under steady conditions, the energy balance of this volume element can be expressed as:

$$\begin{array}{rl}\cancel{\frac{dE}{dt}}& ={\dot{E}}_{\text{in}}-{\dot{E}}_{\text{out}}+\cancel{{\dot{E}}_{\text{gen}}}-\cancel{{\dot{E}}_{\text{consumed}}}\\ {\dot{E}}_{\text{in}}& ={\dot{E}}_{\text{out}}\\ {\dot{Q}}_{\text{cond},x}& ={\dot{Q}}_{\text{cond},x+\Delta x}+{\dot{Q}}_{\text{conv}}\end{array}$$

The second term on the right side, heat transfer from convection, can be written as:

$${\dot{Q}}_{\text{conv}}=h\underset{\text{Area}}{\underbrace{(p\Delta x)}}(T(x)-T_{\infty })$$

For conduction, we can write a Taylor series expansion to relate ${\dot{Q}}_{\text{cond},x}$ and ${\dot{Q}}_{\text{cond},x+\Delta x}$. Omitting the $\text{cond}$ subscript for clarity, we have:

$${\dot{Q}}_{x+\Delta x}\approx {\dot{Q}}_x+\frac{d{\dot{Q}}_x}{dx}\Delta x$$

Combining, we have:

$$\begin{array}{rl}{\dot{Q}}_{\text{cond},x}& ={\dot{Q}}_{\text{cond},x+\Delta x}+{\dot{Q}}_{\text{conv}}\\ {\dot{Q}}_x& ={\dot{Q}}_x+\frac{d{\dot{Q}}_x}{dx}\Delta x+h(p\Delta x)(T(x)-T_{\infty })\end{array}$$

Removing ${\dot{Q}}_x$ from both sides gives:

$$\frac{d{\dot{Q}}_x}{dx}\cancel{\Delta x}+h(p\cancel{\Delta x})(T(x)-T_{\infty })=0$$

From Fourier’s law of heat conduction, we have ${\dot{Q}}_x=-k{A}_c\frac{dT}{dx}$. Substituting this in, we have:

$$\frac{d}{dx}\left(-k{A}_c\frac{dT}{dx}\right)+hp(T(x)-T_{\infty })=0$$

For constant cross-sectional area and constant $k$, this becomes:

$$\boxed{\frac{d^{2}T}{d{x}^2}-\frac{hp}{k{A}_c}(T-T_{\infty })=0}$$

This can be written as:

$$\frac{d^2\theta }{d{x}^2}-m^2\theta =0$$

where $\theta =T-T_{\infty }$, and

$$m=\frac{hp}{k{\mathcal{A}}_c}$$

Fin Equation Solutions

The above is a linear, homogeneous, second-order differential equation with constant coefficients. The general solution is:

$$\theta (x)=C_1{e}^{mx}+C_2{e}^{-mx}$$

We determine $C_1$ and $C_2$ based on various boundary conditions.

It should be noted that the plate to which the fins are attached is normally known in advance. Thus, at the fin base, we have a specified temperature boundary expressed as:

$$\theta (0)={\theta }_b=T_b-T_{\infty }$$

At the fin tip, we have several possibilities, including:

• Very long fins (idealized as infinite long)
• Adiabatic fin tip
• Specified temperature $T$ at fin tip
• Convection at fin tip

With this, we can determine a temperature distribution for the fin:

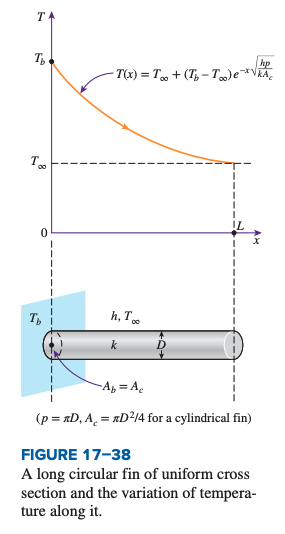
In the example above, we have a very long fin, where there is an exponential decay of temperature as distance from the fin base increases.

Very Long Fin

For a very long fin, the temperature of the fin at the fin tip approaches the environment temperature $T_{\infty }$, and thus $\theta =T-T_{\infty }$ approaches zero:

$$\theta (L)=T(L)-T_{\infty }=0\text{as}L\to \infty$$

Thus, we have:

• General solution: $\theta (x)=C_1{e}^{mx}+C_2{e}^{-mx}$
• Boundary condition 1: $\theta (0)={\theta }_B=C_1+C_2$
• Boundary condition 2: $\theta (L)=0={\lim }_{x\to \infty }{C}_1{e}^{mx}+C_2{e}^{-mx}$

This is satisfied by:

$$\theta (x)=C_2{e}^{-mx}={\theta }_b{e}^{-mx}$$

The variation of temperature along the fin can then be expressed as:

$$\frac{T(x)-T\infty }{T_b-T_{\infty }}=e^{-mx}=e^{-x\sqrt{hp/k{A}_c}}$$

The steady rate of heat transfer from the entire fin is:

$${\dot{Q}}_{\text{long fin}}=-k{A}_c\frac{dT}{dx}{|}_{x=0}=\sqrt{hpk{A}_c}(T_b-T_{\infty })$$

Adiabatic Fin Tip

A more realistic situation is for heat transfer from the fin tip to be negligible, since the heat transfer from the fin is proportional to the fin area. This boundary condition can be expressed as:

$$\frac{d\theta }{dx}{|}_{x=L}=0$$

This can be solved to obtain:

$$\frac{T(x)-T\infty }{T_b-T_{\infty }}=\frac{\cosh m(L-x)}{\cosh mL}$$

The rate of heat transfer from the fin in this case is:

$${\dot{Q}}_{\text{adiabatic tip}}=-k{A}_c\frac{dT}{dx}{|}_{x=0}=\sqrt{hpk{A}_c}(T_b-T_{\infty })\tanh mL$$

Specific Temperature at Fin Tip

In this case, the temperature at the end of the fin is fixed at a specified temperature $T_L$, such that:

$$\theta (L)=T_L-T_{\infty }$$

This can be solved to get:

$$\frac{T(x)-T\infty }{T_b-T_{\infty }}=\frac{[(T_L-T_{\infty })/(T_b-T_{\infty })]\sinh mx+\sinh m(L-x)}{\sinh mL}$$

The rate of heat transfer for this case is:

$$\begin{array}{rl}{\dot{Q}}_{\text{specified temp.}}& =-k{A}_c\frac{dT}{dx}{|}_{x=0}\\ & =\sqrt{hpk{A}_c}(T_b-T_{\infty })\frac{\cosh mL-[(T_L-T_{\infty }/(T_b-T_{\infty })]}{\sinh mL}\end{array}$$

Convection from Fin Tip + Corrected Fin Length

In practice, the fin tips are exposed to the surroundings, so the boundary conditions should include convection. This temperature distribution can be written as:

$$\frac{T(x)-T\infty }{T_b-T_{\infty }}=\frac{\cosh m(L-x)+(h/mk)\sinh m(L-x)}{\cosh mL+(h/mk)\sinh mL}$$

The rate of heat transfer for this case is:

$$\begin{array}{rl}{\dot{Q}}_{\text{specified temp.}}& =-k{A}_c\frac{dT}{dx}{|}_{x=0}\\ & =\sqrt{hpk{A}_c}(T_b-T_{\infty })\frac{\sinh mL+(h/mk)\cosh mL}{\cosh mL+(h/mk)\sinh mL}\end{array}$$

Fin Temperature Distributions

The conduction and convection in a fin occurs as a function of location $x$. See Figure 17-38 above for example. Thus, we cannot use the standard thermal resistance equations for conduction and convection.

‘

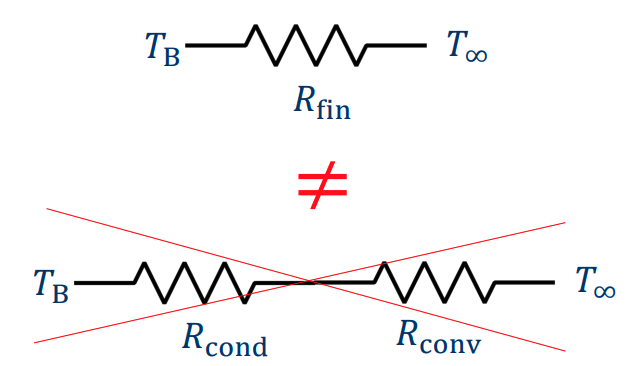
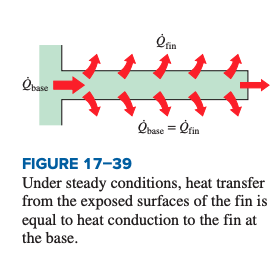Example