Lowpass Filter

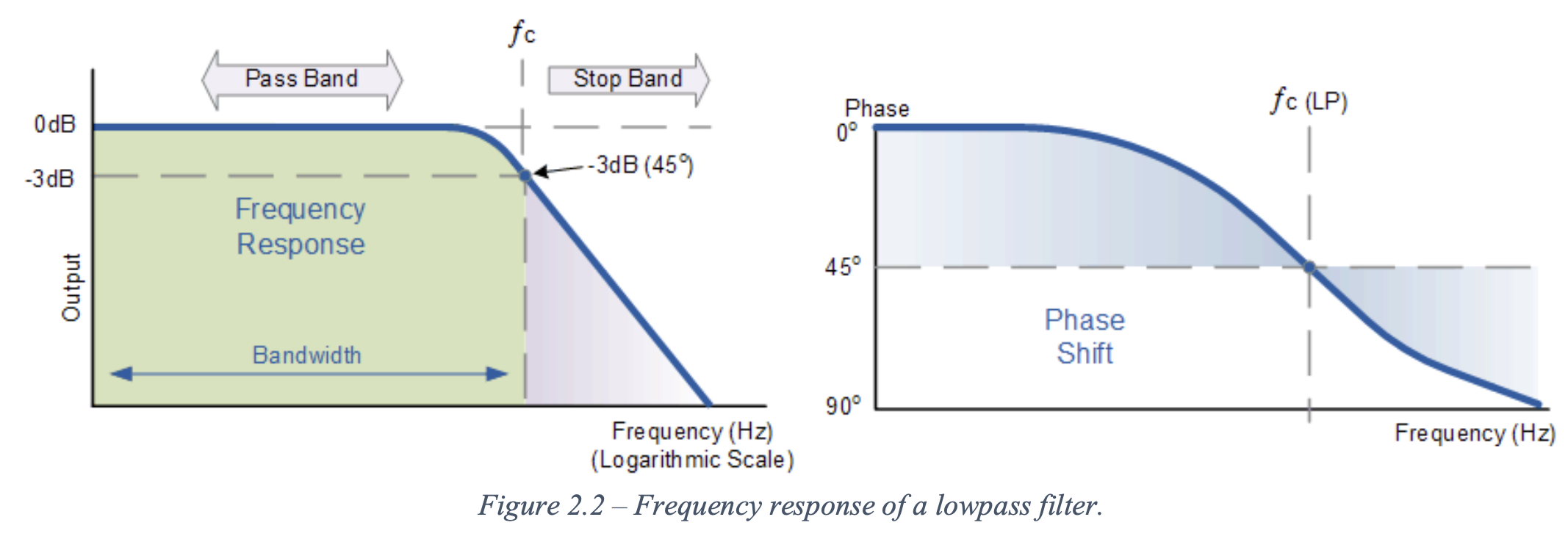
The low pass filter allows low-frequency signals to pass through while attenuating high-frequency components. Commonly used to eliminate noise or smooth out signals.

Corner/cutoff frequency

Frequency above which the filter attenuates the input signal. Defined as ${\omega }_c$ in $\text{[rad/s]}$ or $f_c$ in $\text{[Hz]}$, depends on the time constant of the RC or RC circuit:

$${\omega }_c=2\pi f_c=\frac{1}{\tau }$$

• Allow signals to pass through with minimal attenuation at frequencies below the corner frequency
• Progressively attenuate the signal as the frequency increases above the corner frequency

The corner frequency corresponds to the -3 dB (~0.707 times the maximum value), where the signal loses 50% of its power.

Filters can be active or passive: Passive filters can pass or block frequencies but do not add energy to the signal (gain $\le$ 1). Active filters perform the same frequency functions but can add energy to the signal (gain $>$ 1).

Passive lowpass filter

Consists of passive components such as resistors, capacitors, and inductors and does not require an external power source. First order passive filters are configured like a voltage divider, but one of the resistors is a frequency-dependent impedance instead.

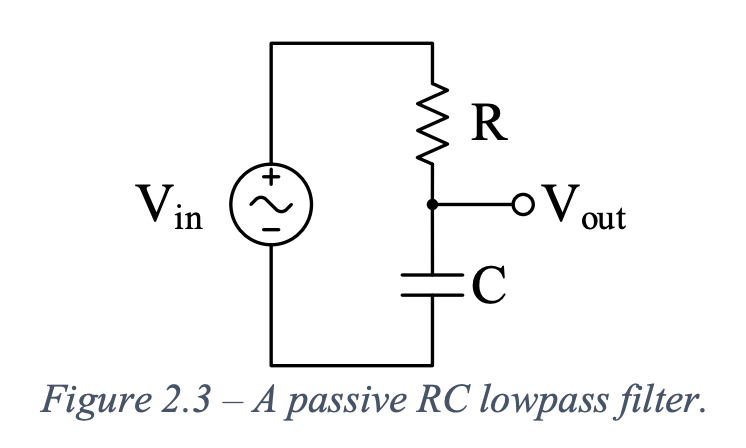
In the figure above, the capacitor’s $Z_c$ looks like an open circuit at low frequencies, so $V_{out}=V_{in}$ and low frequencies pass. At high frequencies, it looks like a short circuit, so $V_{out}=0$, and high frequencies are blocked. Note that output loading changes the corner frequency since the time constant includes the load resistance.

Active highpass filter

An active highpass filter uses an opamp circuit, but the feedback resistance is a frequency-dependent impedance.

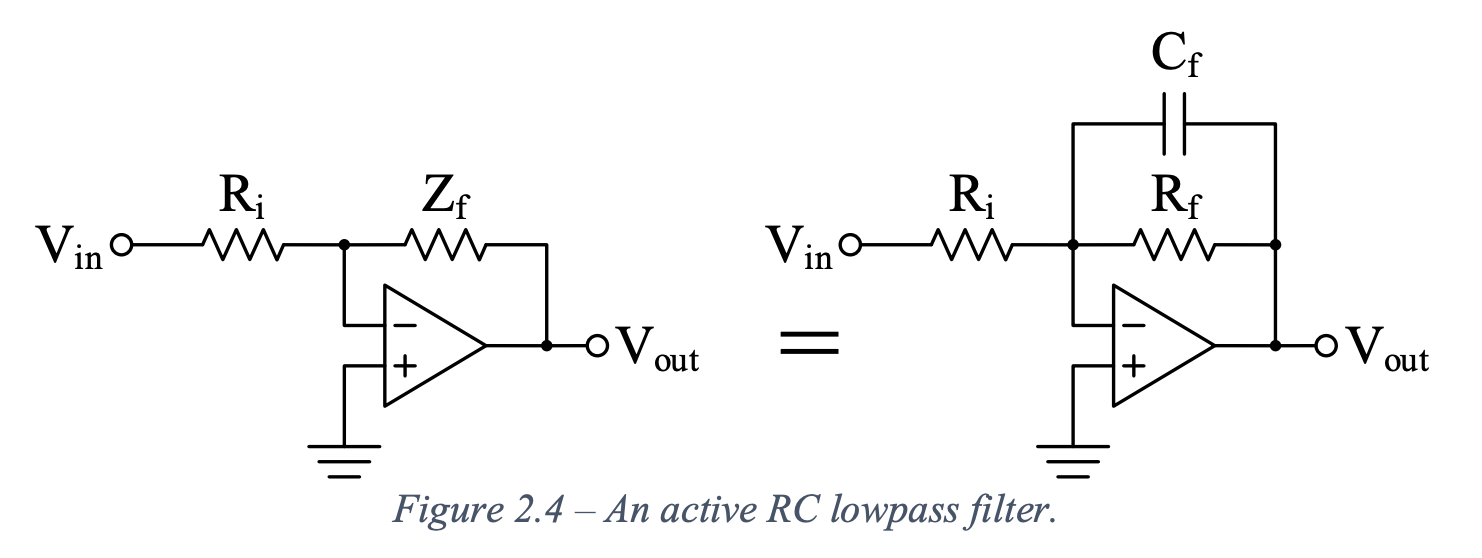
In the figure above, the close loop gain would be $-Z_f/R_i=-(Z_{C_f}\mid \mid R_f)/R_i$. The capacitor’s $Z_c$ looks like an open circuit at low frequencies, so $V_{out}=-(R_f/R_{in})V_{in}$ and low frequencies pass with a gain of $-R_f/R_{in}$. At high frequencies it looks like a short circuit, so $V_{out}=0$, and high frequencies are blocked.

For active filters, the output loading does not change the corner frequency because the op-amp provides isolation between the filter and the load.

The choice between passive and active lowpass filters depends on the desired frequency response, complexity, precision requirements, and available power sources. Passive filters are simpler and suitable for basic filtering applications, while active filters offer more flexibility and improved performance for complex filtering tasks. You will build a passive and an active lowpass filter and study their performance.