Convolutional Layer

Convolutional layers are network layers that perform the convolution operation. In 1D, a convolution transforms an input vector $\mathbf{x}$ into an output vector $\mathbf{z}$ so that each output $z_i$ is a weighted sum of nearby inputs. The same weights are used at every position and are collectively called the convolution layer or filter.

A convolutional layer computes its output by convolving the input, adding a bias $\beta$, and passing each result through an activation function.

For example, with kernel size 3, stride 1, dilation rate 1, the $i$-th hidden unit would be computed as:

$$\begin{array}{rl}{h}_i& =\text{a}[\beta +{\omega }_1{x}_{i-1}+{\omega }_2{x}_i+{\omega }_3{x}_{i+1}]\\ & =\text{a}\left[\beta +\sum _{j=1}^3{\omega }_j{x}_{i+j-2}\right]\end{array}$$

where the bias $\beta$ and the kernel weights ${\omega }_1,{\omega }_2,{\omega }_3$ are trainable weights, and we treat the input $x$ as zero when it is out of the valid range (zero padding).

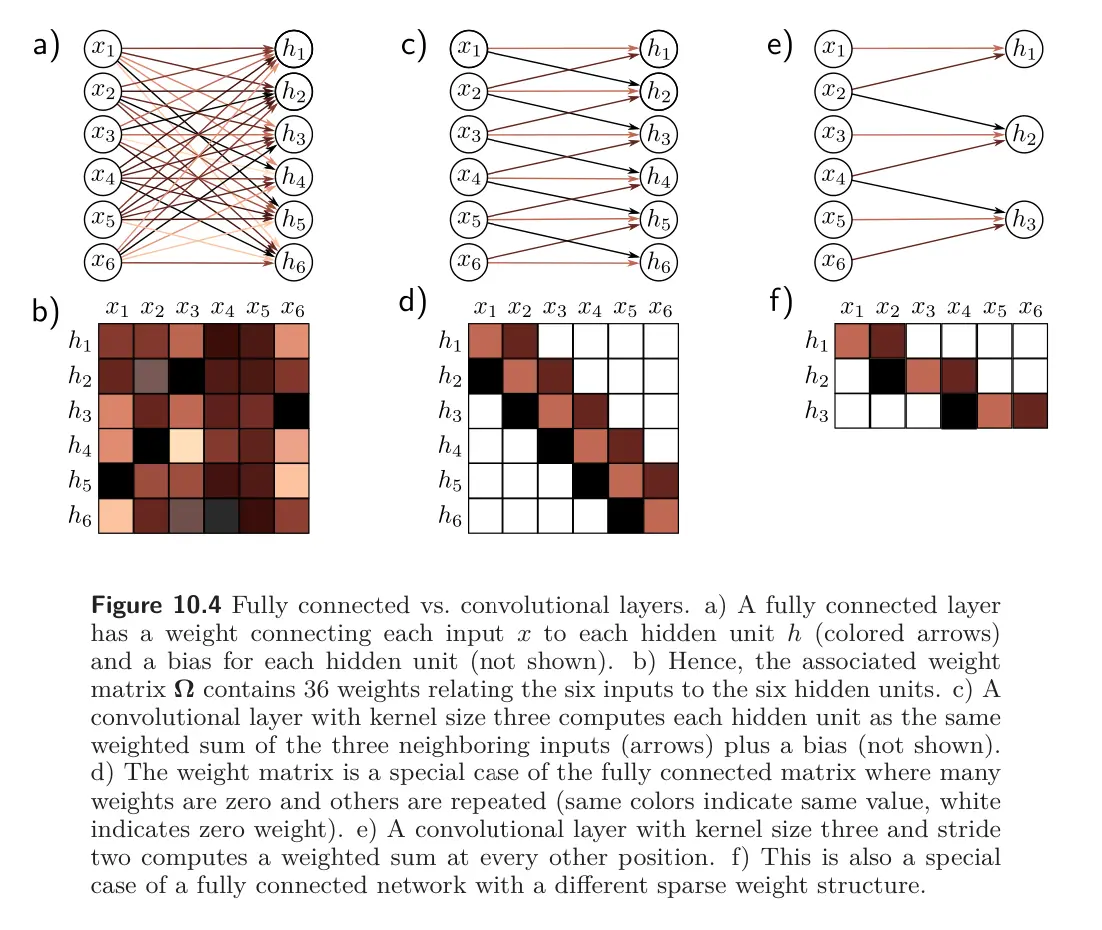
Convolutional vs. fully-connected layers

We can view this as a special case of a fully connected layer that computes the $i$-th hidden unit as:

$$h_i=\text{a}\left[{\beta }_i+\sum _{j=1}^D{\omega }_{ij}{x}_i\right]$$

If there are $D$ inputs $x_{\bullet }$ and $D$ hidden units $h_{\bullet }$, this fully connected layer would have $D^2$ weights ${\omega }_{\bullet \bullet }$ and $D$ biases ${\beta }_{\bullet }$. The convolutional layer only uses 3 weights and 1 bias. A fully connected weight can reproduce this if most weights are set to zero and others are constrained to be identical.

Convolutions as image filter banks

Each 2D convolution operation performs as an Image Filter. We can stack multiple convolutions on top of each other (channels), such that we lose less information while being much more efficient than a FC layer in terms of number of weights.

The goal is to have each filter (conv kernel) of an Image Filter Bank correspond to a single neural network layer. Each filter corresponds to one output feature map (channel).

The same weights are used many many times in the computation of each layer. This weight sharing means that we can express a transformation on a large image with relatively few parameters; it also means we’ll have to take care in figuring out exactly how to train it.

A convolution layer/filter layer is formally defined with:

• Number of filters $m^l$
• Size of one filter is $k^l\times k^l\times m^{l-1}$ (plus 1 bias value for this kernel)
• Stride $s^l$ is the spacing at which we apply the filter to the image
• Input tensor size $n^{l-1}\times n^{l-1}\times m^{l-1}$
• Padding $p^l$ is how many extra pixels (usually with value $0$) are added around the edges of the input. For an input of size $n^{l-1}\times n^{l-1}\times m^{l-1}$, our new effective input size with padding becomes $(n^{l-1}+2\cdot p^l)\times (n^{l-1}+2\cdot p^l)\times m^{l-1}$

This layer will produce an output of size $n^l\times n^l\times m^l$, where

$$n^l=\lceil \frac{n^{l-1}+2\cdot p^l-(k^l-1)}{s^l}\rceil$$

Any bias terms are simply applied with element-wise addition.