Convolutional layers are network layers that perform the convolution operation. In 1D, a convolution transforms an input vector into an output vector so that each output is a weighted sum of nearby inputs. The same weights are used at every position and are collectively called the convolutional layer or filter.
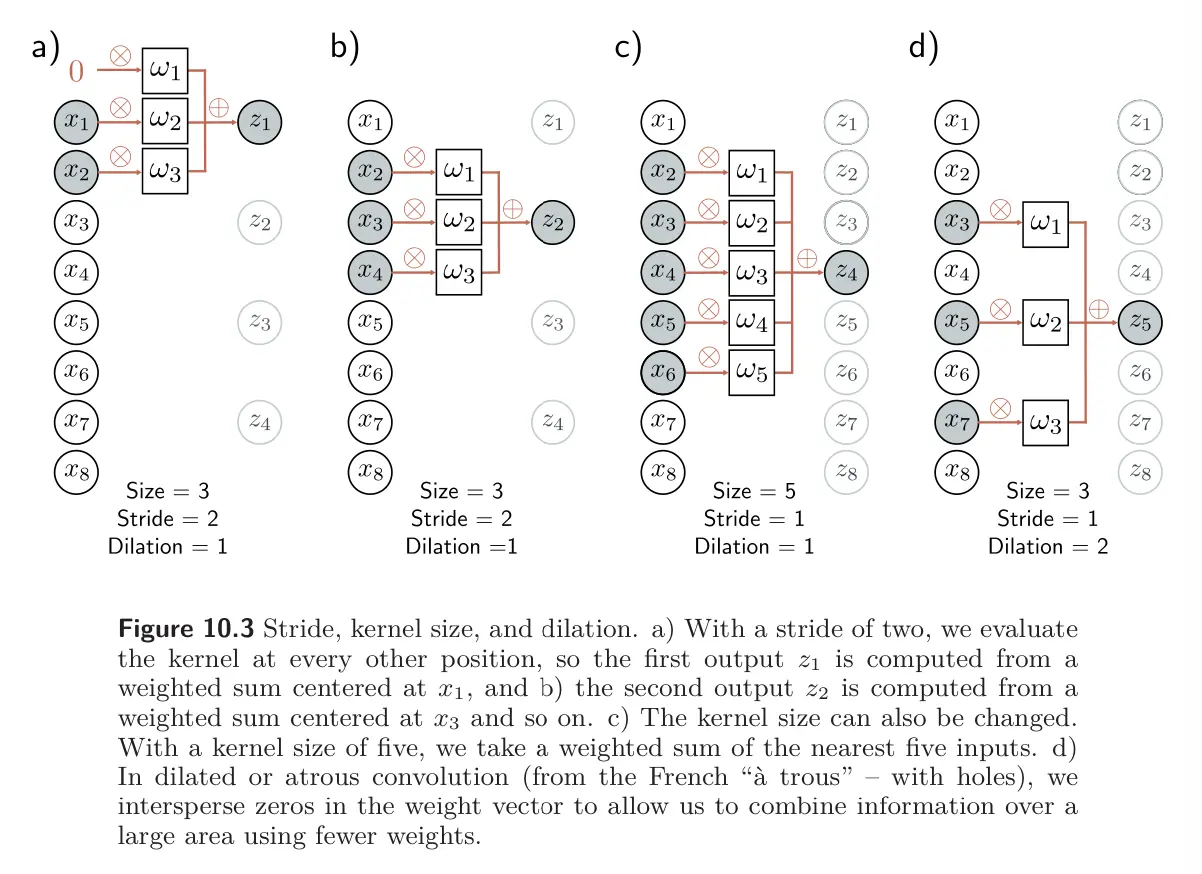
The size of the region over which inputs are combined is termed the kernel size. For a kernel size of 3, we have:
where is the kernel.
Note that the convolution operation is equivariant with respect to translation. If we translate the input , then the corresponding output is translated in the same way.
Padding
As we saw from the equation above, each output is computed by taking a weighted sum of the previous, current, and subsequent positions in the input. Then, how do we deal with the first output, where there is no previous input? How do we deal with the final output, where there is no subsequent input?
We can pad the edges of the inputs with new values and proceed as usual. Zero-padding assumes the input is zero outside of its valid range. Other possibilities include treating the input as circular or reflecting at the boundaries.
Another option is to discard the output positions where the kernel exceeds the input positions. These valid convolutions have the advantage of introducing no extra information at the edges of the input. However, they have the disadvantage that the representation decreases in size.
Stride, kernel size, dilation rate
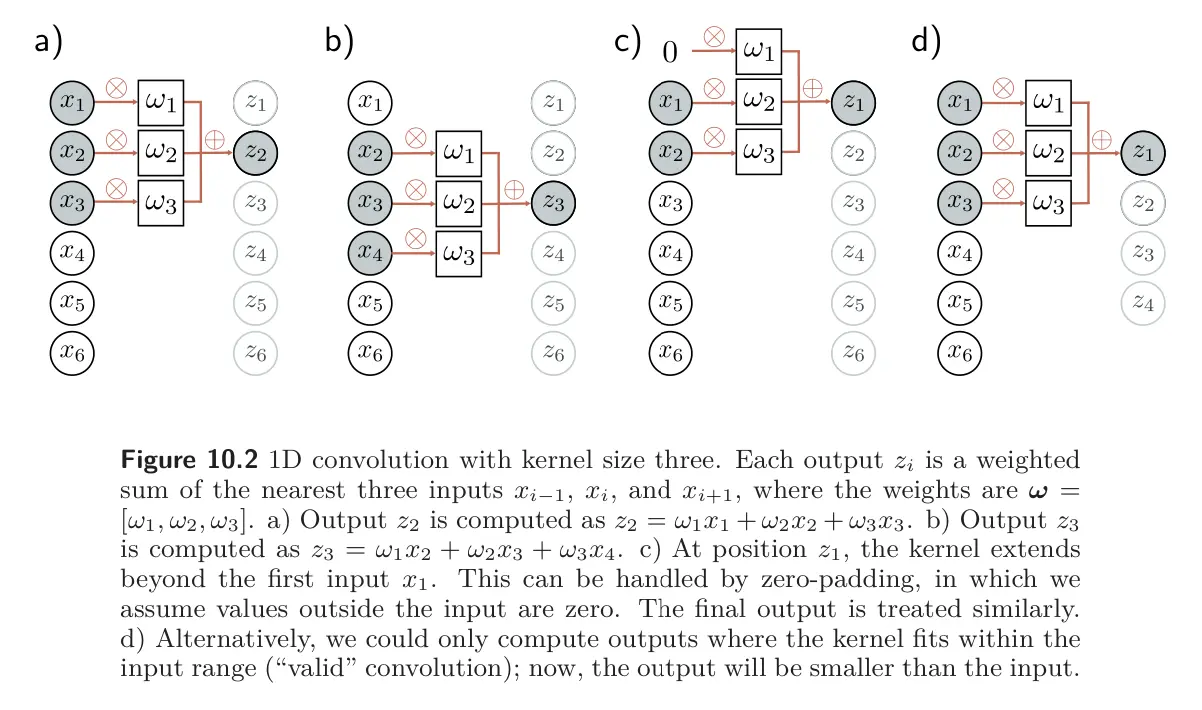
We can characterize a larger family of convolution operations by their stride, kernel size, and dilation rate.
Stride: When we evaluate the output at every position, this is a stride of one. We can also shift the kernel by a stride greater than one. If we have a stride of two, we create roughly half the number of outputs.
Kernel size: The kernel size can be increased to integrate over a larger area. However, it typically remains an odd number so that it can be centered around the current position. Increasing the kernel size has the disadvantage of requiring more weights.
Dilation: In dilated/atrous convolutions, the kernel values are interspersed with zeros. For example, we can turn a kernel of size 5 into a dilated kernel of size 3 by setting the 2nd and 4th elements to zero. We still integrate information from a larger input region but only require three weights to do this. The number of zeros we intersperse between the weights determines the dilation rate.