Image Filter Bank

A filter bank is a set of sets of filters, arranged as shown in the diagram below:

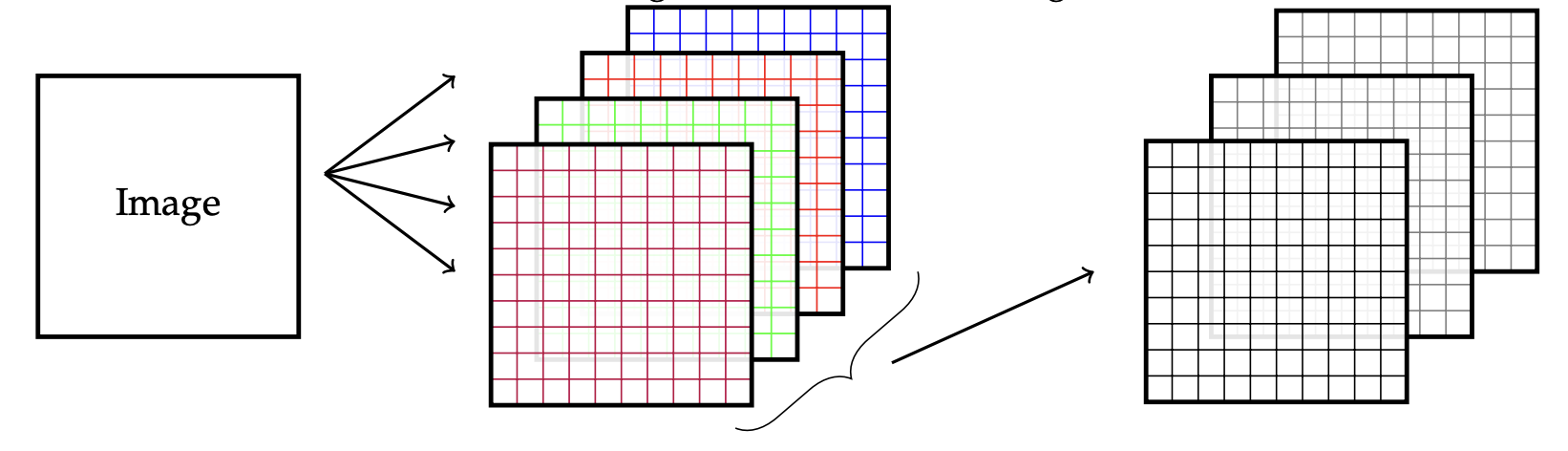
All filters are applied to the image (see 2D Convolution Operation). If there are $k$ filters, the result is $k$ images, which are called channels. These are then “stacked” to form a cube of data, indexed by (row, column, index). The next set of filters will then be three-dimensional; each one is applied to a sub-range of the row and column indices of the image and to all of the channels. These 3D chunks of data are called tensors.

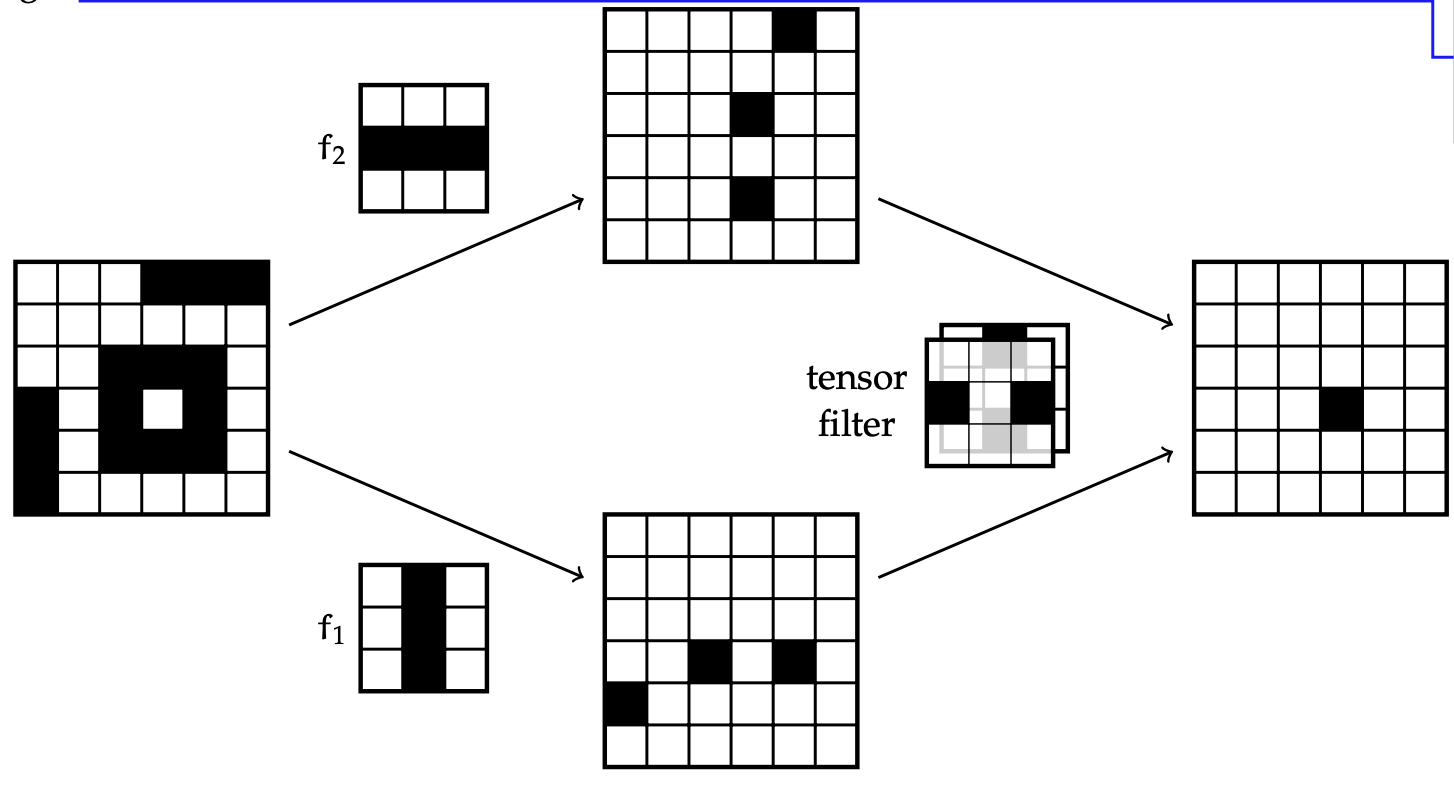
A more concrete (but still simple) example with an $6\times 6$ image

• $f_1$ “looks for” 3 vertical pixels in a row
• $f_2$ “looks for” 3 horizontal pixels in a row
• Both $f_1$ and $f_2$ are applied with stride $1$ and $1\times 1$ padding to produce $6\times 6$ channels
• The result of filtering with $f_1$ and $f_2$ is a 3D tensor ($6\times 6\times 2$)
• We can then apply a $3\times 3\times 2$ tensor filter that “looks for” a combination of two horizontal and two vertical bars, now represented by individual pixels in the two channels.

Filter banks are often structured into a pyramid, in which the images get smaller in successive layers of processing. The idea is that we can find local patterns, like bits of edges in early layers, and then look for patterns in those patterns, etc. This means that, effectively, we are looking for patterns in larger pieces of the image as we apply successive filters. Having a stride greater than one makes the images smaller, but does not necessarily aggregate information over that spatial range.