IOP with SPA

Recall that the IOP equations are:

$$\begin{array}{r}X+GW=1\\ V+GX=0\end{array}$$

Then, we can write a simple pole approximation of $W[z]$ as:

$$W[z]=\sum _{i=1}^m\frac{w_i}{z-p_i}$$

We can also write a plant $G[z]$ with simple poles as:

$$G[z]=\sum _{k=1}^n\frac{c_k}{z-q_k}$$

where we split its poles into stable and unstable components $\{q_k{\}}_{k=1}^{\hat{n}}$ and $\{q_k{\}}_{k=\hat{n}+1}^n$.

With that setting, we can write $X$ as partial fraction decomposition

$$X[z]=1+\sum _{i=1}^m\frac{x_i}{z-p_i}+\sum _{k=1}^{\hat{n}}\frac{{\hat{x}}_k}{z-q_k}$$

We can then write the first IOP equation $X+GW=1$ as:

$$\begin{array}{rl}{x}_i& =-{\alpha }_i{w}_i\forall i\in \{1,\dots ,m\}\\ {\hat{x}}_k& =\sum _{i=1}^m-{\beta }_{k,i}{w}_i\forall k\in \{1,\dots ,\hat{n}\}\\ 0& =\sum _{i=1}^m-{\beta }_{k,1}{w}_i\forall k\in \{\hat{n}+1,\dots ,n\}\end{array}$$

The second IOP equation can in turn be written as:

$$\begin{array}{r}0=-c_j+\sum _{i=1}^m-{\gamma }_{j,i}{x}_i+\sum _{k=1}^{\hat{n}}-{\hat{\gamma }}_{j,k}{\hat{x}}_k\forall j\in \{\hat{n}+1,n\}\end{array}$$

With this formulation, we can also define Specs for Control Design.

Vector Form

Define

$$w:=\left[\begin{array}{c}{w}_1\\ ⋮\\ w_m\end{array}\right],x:=\left[\begin{array}{c}{x}_1\\ ⋮\\ x_m\end{array}\right],\hat{x}:=\left[\begin{array}{c}{\hat{x}}_1\\ ⋮\\ {\hat{x}}_{\hat{n}}\end{array}\right]$$

where $w$ is the coefficients in our SPA form of $W$, and similarly $x,\hat{x}$ are the coefficients in $X.$

Define

$$\alpha :=\left[\begin{array}{ccc}{\alpha }_1& \dots & 0\\ & \ddots & \\ 0& \dots & {\alpha }_m\end{array}\right]$$

where the diagonal terms are ${\alpha }_1,\dots ,{\alpha }_m$ and everything else is $0$.

Define

$$\beta :=\left[\begin{array}{ccc}{\beta }_{1,1}& \dots & {\beta }_{1,m}\\ ⋮& & ⋮\\ {\beta }_{\hat{n},1}& \dots & {\beta }_{\hat{n},m}\\ ⋮& & ⋮\\ {\beta }_{n,1}& \dots & {\beta }_{n,m}\end{array}\right]$$

and

$$\gamma :=\left[\begin{array}{ccc}{\gamma }_{\hat{n}+1,1}& \dots & {\gamma }_{\hat{n}+1,m}\\ ⋮& & ⋮\\ {\gamma }_{n,1}& \dots & {\gamma }_{n,m}\end{array}\right],\hat{\gamma }:=\left[\begin{array}{ccc}{\hat{\gamma }}_{\hat{n}+1,1}& \dots & {\hat{\gamma }}_{\hat{n}+1,m}\\ ⋮& & ⋮\\ {\hat{\gamma }}_{n,1}& \dots & {\hat{\gamma }}_{n,m}\end{array}\right]$$

As an example, if we had $n=3,\hat{n}=1,m=3$:

$$\gamma :=\left[\begin{array}{ccc}{\gamma }_{2,1}& {\gamma }_{2,2}& {\gamma }_{2,3}\\ {\gamma }_{3,1}& {\gamma }_{3,2}& {\gamma }_{3,3}\end{array}\right]$$

Now we can re-express our IOP equations in terms of these vectors and matrices. Notice that $\alpha ,\beta ,\gamma ,\hat{\gamma }$ are all constants. The only variables are $w,x,\hat{x}$. Re-arranging our above equations:

$$\begin{array}{rl}{x}_i+{\alpha }_i{w}_i& =0\forall i\in \{1,\dots ,m\}\\ {\hat{x}}_k+\sum _{i=1}^m{\beta }_{k,i}{w}_i& =0\forall k\in \{1,\dots ,\hat{n}\}\\ \sum _{i=1}^m{\beta }_{k,1}{w}_i& =0\forall k\in \{\hat{n}+1,\dots ,n\}\\ \sum _{i=1}^m{\gamma }_{j,i}{x}_i+\sum _{k=1}^{\hat{n}}{\hat{\gamma }}_{j,k}{\hat{x}}_k& =-c_j\forall j\in \{\hat{n}+1,n\}\end{array}$$

Converting to matrix form:

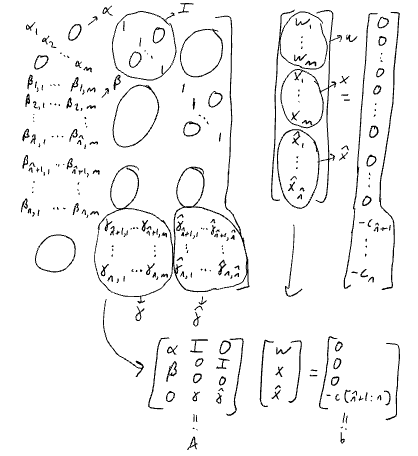
So we have:

$$\begin{array}{rl}\left[\begin{array}{ccc}\alpha & I& 0\\ \beta & 0& I\\ ⋮& 0& 0\\ 0& \gamma & \hat{\gamma }\end{array}\right]\left[\begin{array}{c}w\\ x\\ \hat{x}\end{array}\right]& =\left[\begin{array}{c}0\\ 0\\ 0\\ -c[\hat{n}+1:n]\end{array}\right]\\ A\left[\begin{array}{c}w\\ x\\ \hat{x}\end{array}\right]& =b\end{array}$$