Closed-Loop Stability

Continuous-time and discrete-time feedback control systems take the following general forms:

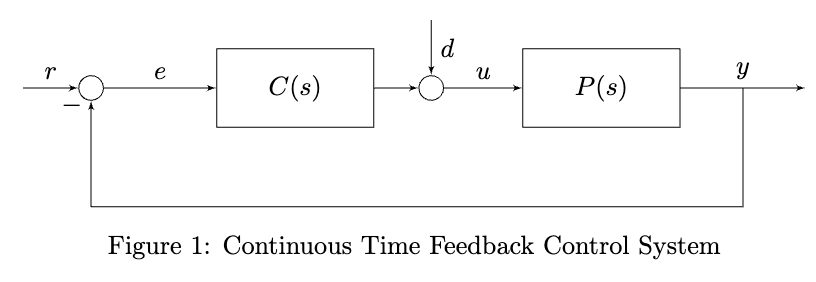
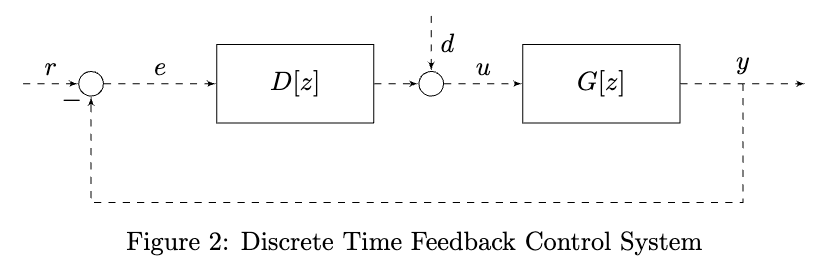
• $C(s)/D[z]$ are controller
• $P(s)/G[z]$ are plant

The systems have many different transfer functions. To distinguish these, we make the distinction between external and internal signals:

• External signals: $r,d$ – we have no control over these
• Internal signals: $u,e,y$ – these depend on our control design

We consider transfer functions from external signals to internal signals (closed-loop transfer functions):

$$T_{ry},T_{re},T_{ru},T_{dy},T_{de},T_{du}$$

• We consider external-to-internal TFs because our goal is to understand the influence of external factors on the internals of our system

Example:

$$\begin{array}{rl}y& =Pu=P(d+Ce)=P(d+C(r-y))\\ & ⟹y=Pd+PCr-PCy\\ & ⟹(1+PC)y=Pd+PCr\\ & ⟹y=\underset{T_{dy}}{\underbrace{\frac{P}{1+PC}}}d+\underset{T_{ry}}{\underbrace{\frac{PC}{1+PC}}}r\end{array}$$

We can generalize these in matrix form for both continuous and discrete time:

$$\begin{array}{r}\text{Continuous-time:}\left[\begin{array}{c}U\\ E\\ Y\end{array}\right]=\left[\begin{array}{cc}\frac{C}{1+PC}& \frac{1}{1+PC}\\ \frac{1}{1+PC}& \frac{-P}{1+PC}\\ \frac{PC}{1+PC}& \frac{P}{1+PC}\end{array}\right]\left[\begin{array}{c}R\\ D\end{array}\right]\\ \text{Discrete-time:}\left[\begin{array}{c}U\\ E\\ Y\end{array}\right]=\left[\begin{array}{cc}\frac{D}{1+GD}& \frac{1}{1+GD}\\ \frac{1}{1+GD}& \frac{-G}{1+GD}\\ \frac{GD}{1+GD}& \frac{G}{1+GD}\end{array}\right]\left[\begin{array}{c}R\\ D\end{array}\right]\end{array}$$

Well-posed

A feedback system is well-posed if all closed-loop transfer function from external signals to internal signals are real, rational, and proper.

Closed-loop stable / Internally stable

A closed-loop system is closed-loop stable or internally stable if all closed-loop transfer functions from external signals to internal signals $T_{ry},T_{re},T_{ru},T_{dy},T_{de},T_{du}$ are BIBO stable.

• This is equivalent to saying that for any bounded external signals $r,d$, the internal signals $u,e,y$ are bounded as well.
• As $e=r-y$ is bounded whenever $r,y$ is bounded whenever $r,y$ are bounded, it suffices to only consider the 4 transfer functions from $(r,d)$ to $(u,y)$ to determine closed-loop stability.
• Equivalently, as $y=r-e$ is bounded whenever $r,e$ are bounded, it suffices to only consider the 4 transfer functions from $(r,d)$ to $(u,e)$ to determine closed-loop stability.

Examples

Example 1: Suppose $G[z]=\frac{z+2}{\left(z+\frac{1}{2}\right)(z-1)},D[z]=\frac{1}{z+2}$.

We have:

$$\begin{array}{r}{T}_{ry}=\frac{GD}{1+GD}=\cdots =\frac{1}{z^2-\frac{1}{2}z+\frac{1}{2}}\end{array}$$

Then:

$$\text{Poles}(T_{ry})\subset \mathbb{D}$$

So $T_{ry}$ is stable (definition of stability). In turn, $T_{ry}$ is BIBO stable (theorem from class).

However, it can be shown that this system is NOT closed-loop stable! (Because $T_{ru}$ is unstable.)

Example 2:

$$G[z]=\frac{z+\frac{1}{2}}{z+2},D[z]=\frac{z-1}{z+\frac{1}{2}}$$

• Unstable plant, stable controller

Checking the transfer functions:

$$\begin{array}{rl}{T}_{ry}& =\frac{GD}{1+GD}=\frac{z-1}{2z+1}\\ T_{dy}& =\frac{G}{1+GD}=\frac{z+\frac{1}{2}}{2z+1}\\ T_{ru}& =\frac{D}{1+GD}=\frac{(z-1)(z+2)}{\left(z+\frac{1}{2}\right)(2z+1)}\\ T_{du}& =\frac{1}{1+GD}=\frac{z+2}{2z+1}\end{array}$$

Thus, the system is closed-loop stable!

Example 3:

$$G[z]=\frac{z-4}{z+2},D[z]=\frac{z+1}{z+2}$$

This system is closed-loop stable, despite having an unstable plant and an unstable controller.

Example 4:

$$G[z]=\frac{z+3}{z+\frac{1}{2}},D[z]=\frac{z+2}{z-\frac{1}{2}}$$

This stable is not closed-loop stable, despite having stable plant and controller.

Thus, it is not always intuitive in feedback systems whether the system will be closed-loop stable even if both the plant and controller are closed-loop stable.