Sept 30 IOP Tutorial

Example 4.1: Closed-loop stability

Consider the following standard negative feedback system:

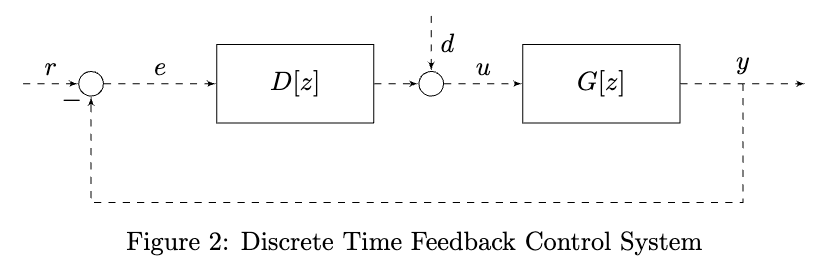
where we have

$$\begin{array}{rl}D[z]& =\frac{(z-1)\left(z-\frac{1}{2}\right)}{(2z+1)(5z-2)}\\ G[z]& =\frac{z+1}{(4z-3)\left(z-\frac{1}{2}\right)}\end{array}$$

To check closed-loop stability, we need to check the closed-loop transfer functions.

$$T_{re}=T_{du}=\frac{1}{1+GD}=\frac{(4z-3)(2z+1)(5z-2)}{40z^3-25z^2-11z+5}$$

• Roots: -0.48, 0.34, 0.77

$$T_{ru}=\frac{D}{1+GD}=\frac{(4z-3)(z-1)\left(z-\frac{1}{2}\right)}{40z^3-25z^2-11z+5}$$

• Roots: -0.48, 0.34, 0.77

$$T_{de}=\frac{-G}{1+GD}=\frac{-(z+1)(2z+1)(5z-2)}{\left(z-\frac{1}{2}\right)(40z^3-25z^2-11z+5)}$$

• Roots: -0.48, 0.34, 0.5, 0.77

Then:

• $T_{re},T_{du},T_{ru},T_{de}$ are real, rational and proper.
• Since the poles of these lie in the open unit disk the TFs are stable [definition of stability].
• These TFs are BIBO stable [theorem from class]
• The system is closed-loop stable [definition of closed-loop stability]

IOP Theorem

Theorem IOPa.

If $D[z]$ results in closed-loop stability, then $X[z]=T_{re}=T_{du}$, $W[z]=T_{ru}$, $V[z]=T_{de}$, satisfying the IOP equations:

$$\begin{array}{rl}& X[z]+G[z]W[z]=1\\ & V[z]+G[z]X[z]=0\\ & X,W,V\text{ are real, rational, and stable.}\end{array}$$

Let’s check for our example above:

$$\begin{array}{rl}X[z]+G[z]W[z]& =\frac{(4z-3)(2z+1)(5z-2)}{40z^3-25z^2-11z+5}+\frac{z+1}{\cancel{(4z-3)}\cancel{\left(z-\frac{1}{2}\right)}}\frac{\cancel{(4z-3)}(z-1)\cancel{\left(z-\frac{1}{2}\right)}}{40z^3-25z^2-11z+5}\\ & =\frac{(4z-3)(2z+1)(5z-2)+(z+1)(z-1)}{40z^3-25z^2-11z+5}\\ & =1\end{array}$$

Similarly, we can show that $V[z]=G[z]X[z]$.

The equations makes sense because

$$\begin{array}{rl}X[z]+G[z]W[z]& =\frac{1}{1+GD}+G\frac{1}{1+GD}=\frac{1+GD}{1+GD}=1\\ V[z]+G[z]X[z]& =\frac{-G}{1+GD}+G\frac{1}{1+GD}=\frac{-G+G}{1+GD}=0\end{array}$$

Theorem IOPb.

If $X[z],W[z],V[z]$ satisfy the IOP equations (i)-(iii) and we choose $D[z]=\frac{W[z]}{X[z]}$, then $T_{re}=T_{du}=X[z]$, $T_{ru}[z]=W[z]$, and $T_{de}[z]=V[z]$.

Example 4.2

Given some “arbitrary” TFs, $X,W,V$, satisfy IOP equations, Solve for $D[z]$, Verify that the CLTF = $X,W,V$.

Example 4.3: SPA

Assume that our plant $G[z]$ only has simple poles, such that:

$$G[z]=\sum _{k=1}^n\frac{c_k}{z-q_k}$$

• Simple pole = poles that are not repeating

Then, we approximate $W[z]$ to be

$$W[z]=\sum _{i=1}^m\frac{w_i}{z-p_i}$$

Then, solving for $X[z]$ from $X[z]+G[z]W[z]=1$ gives:

$$\begin{array}{rl}X[z]& =1+\sum _{k=1}^{\hat{n}}\frac{{\hat{x}}_k}{z-q_k}+\sum _{i=1}^m\frac{x_i}{z-p_i}\\ & =\{\begin{array}{ll}{x}_i=-{\alpha }_i{w}_i& \forall i\in \{1,\dots ,m\}\\ {\hat{x}}_k={\sum }_{i=1}^m-{\beta }_{k,1}{w}_i& \forall k\in \{1,\dots ,\hat{n}\}\\ 0={\sum }_{i=1}^m-{\beta }_{k,i}{w}_i& \end{array}\end{array}$$

• The poles from $1$ to $\hat{n}$ are the stable poles
• The last term is the unstable poles from $W[z]$

We have: