Stable Gain Determination from Nyquist Plots

Given some controller parameter $K$, how can we use a Nyquist plot to determine what values of $K$ will result in a closed-loop stable system?

Consider the following example:

$$\begin{array}{r}G[z]=\frac{1}{z-2},D[z]=K\frac{z+3}{z}\\ L[z]=G[z]D[z]=K\frac{z+3}{z(z-2)}\end{array}$$

To plot $\Gamma$ we use Nyquist(L):

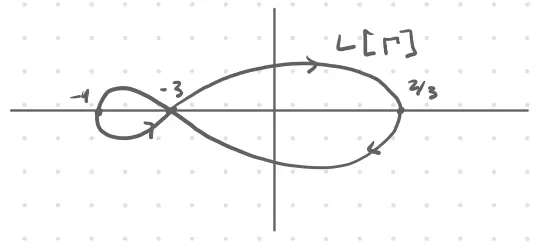
This tells us that with $K=1$, we have $N=-1$ encirclements of the origin. The system one unstable open-loop pole ($z=2$). Thus, since $N\ne \text{number of unstable OL poles}$, the system is not closed-loop stable.

Now, if we vary $K$, where can we find closed-loop stability?

Recall that $V[z]=1+KL[z]$. Via the Argument Principle, We said:

$$\begin{array}{r}\text{Number of encirclements of 0 by }V[\Gamma ]=1+KL[\Gamma ]\\ =\text{Number of encirclements of -1 by }KL[\Gamma ]\\ =\text{Number of encirclements of }-\frac{1}{K}\text{ by }L[\Gamma ]\end{array}$$

• when we change $K$, we don’t have to change the Nyquist plot, just the point around which we count encirclements!

Assume $K\in \mathbb{R}$. To find when the system is stable, we find valid regions on the real axis, which are bounded by points where the Nyquist plot intersects with the real axis.

Region	N
A	0
B	1
C	-1
0	0

We get closed-loop stability when $N$ is equal to the number of unstable open-loop poles (1 in this example). Thus, we get stability when $-\frac{1}{K}$ falls in region $B$, such that:

$$\begin{array}{r}-\frac{1}{K}\in (-4,-3)\\ -4<-\frac{1}{K}<-3\\ 4>\frac{1}{K}>3\\ \frac{1}{4}<K<\frac{1}{3}\end{array}$$

Thus, the system is stable for $K\in \left(\frac{1}{4},\frac{1}{3}\right)$. Note that the Nyquist plot is inconclusive on the boundary points.