Argument Principle

Recall from Contours in Complex Plane that we developed:

$$\frac{1}{2\pi j}\oint \frac{d}{dz}(\log G[z])dz=Z-P$$

where:

• The left side integral is equal to $N$, which is the number of times $G[\Gamma ]$ circles the origin (counterclockwise)
• $Z$ is the number of zeros enclosed by $\Gamma$
• $P$ is the number of poles enclosed by $\Gamma$

This leads to the following lemma:

Lemma: The Argument Principle

Let $\Gamma$ be a contour and $G[z]$ be real, rational, and proper. Then:

$$N=Z-P$$

How does this relate to stability?

Consider the system:

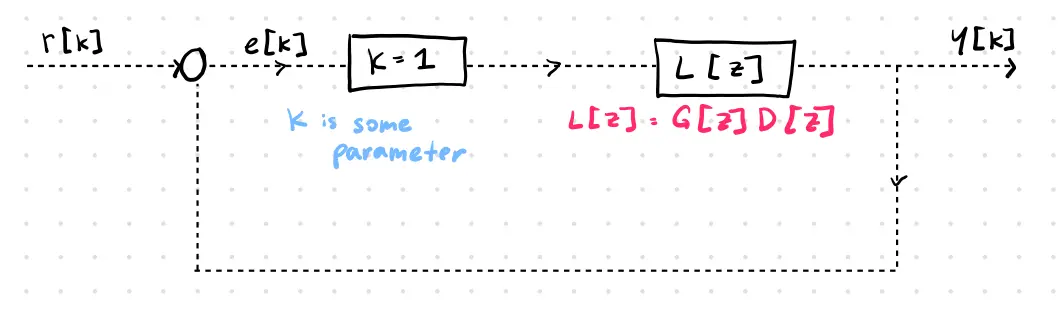
Choose $\Gamma$ to be the unit circle (traversing in the positive direction). Choose $V[z]=1+KL[z]$, such that

$$\begin{array}{rl}K=1⟶V[z]& =1+L[z]\\ & =1+D[z]G[z]\\ & =1+\frac{M[z]f[z]}{N[z]g[z]}\\ & =\frac{M[z]f[z]+N[z]g[z]}{N[z]g[z]}\\ & =\frac{\Delta [z]}{N[z]g[z]}\end{array}$$

Using our earlier integral on $\Gamma$ and $V[z]$:

$$\begin{array}{r}\frac{1}{2\pi j}{\oint }_{\Gamma }(\log V[z])dz=Z-P=N\\ ⟹N=Z-P\end{array}$$

• where $N$ is the number of times $V[\Gamma ]=1+L[\Gamma ]$ encircles $0$
• $Z$ is the number of $\text{roots}(V[z])$ that lie inside $\mathbb{D}$ – stable closed-loop poles
• $P$ is the number of $\text{poles}(V[z])$ that lie inside $\mathbb{D}$ – stable open-loop poles

Note that we can “shift” the argument principle: The number of encirclements of $0$ by $G[\Gamma ]$ is equal to the number of encirclements of $-1$ by $G[\Gamma ]-1$. This leads to the Nyquist Stability Theorem