Edge Detection Filters

Edge detection filters are one of the most fundamental filters. At edges, the pixel intensity changes rapidly. This significant change occurring is conceptually similar to a high-pass filter, whereas smoothing filters were low-pass.

Edge detection is primarily used for to reduce information by keeping structure and discarding detail, providing an an outline/map of major shapes in the scene. - Extract edge ⇒ suppress nonmaxima ⇒ threshold

To find where changes occur, we compute a derivative of the image. Recall from calculus:

$$f^{\prime }(t)=\underset{k\to 0}{\lim }\frac{f(t+h)-f(t)}{h}$$

In digital images, we approximate this using finite differences:

$$f’(t)\approx \frac{f(t+\Delta t)-f(t)}{\Delta t}$$

But now our function is 2D, $I(x,y)$, so we compute derivatives along $x$ and $y$.

A simple discrete derivative filter in 1D would look like:

$$\frac{\partial I}{\partial x}\approx \frac{1}{2}\left[\begin{array}{ccc}-1& 0& 1\end{array}\right]$$

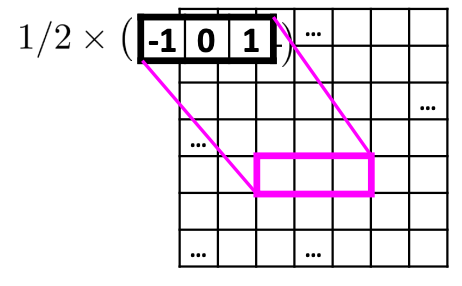
This kernel basically tells us to look at the pixel to the right, subtract the pixel to the left, and ignore the center pixel; this highlights horizontal changes.

One issue is that a raw derivative filter reacts to any change, including random noise. So, before edge detection, we smoothen the image first.

Sobel Edge Detector

A Sobel filter combines Gaussian smoothing and the image derivative. We first apply the horizontal derivative, then a Gaussian smoothing filter. The associativity of convolution filters lets us combine them into one filter. We then also do the same thing in the vertical direction.

This filter detects vertical edges (horizontal intensity change):

$$I_x=\left[\begin{array}{ccc}-1& 0& 1\\ -2& 0& 2\\ -1& 0& 1\end{array}\right]$$

This filter detects horizontal edges (vertical intensity change):

$$I_y=\left[\begin{array}{ccc}-1& -2& -1\\ 0& 0& 0\\ 1& 2& 1\end{array}\right]$$

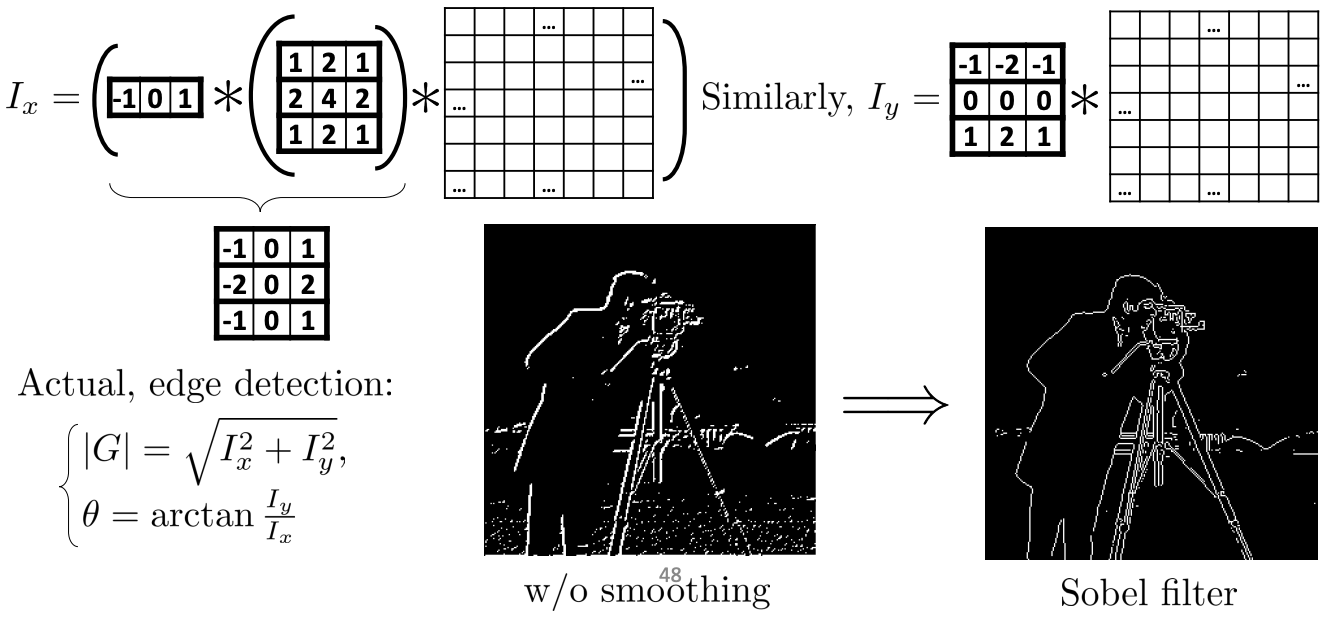
• As we can see, Sobel looks much cleaner than just the raw derivatives!

After applying the two above filters, we can get gradient components $I_x(x,y),I_y(x,y)$. The magnitude of the edge is then given by

$$|G|=\sqrt{I_x^2+I_y^2}$$

and the direction/orientation of the edge is given by:

$$\theta =\arctan \left(\frac{I_y}{I_x}\right)$$