Correlation and Convolution Filters

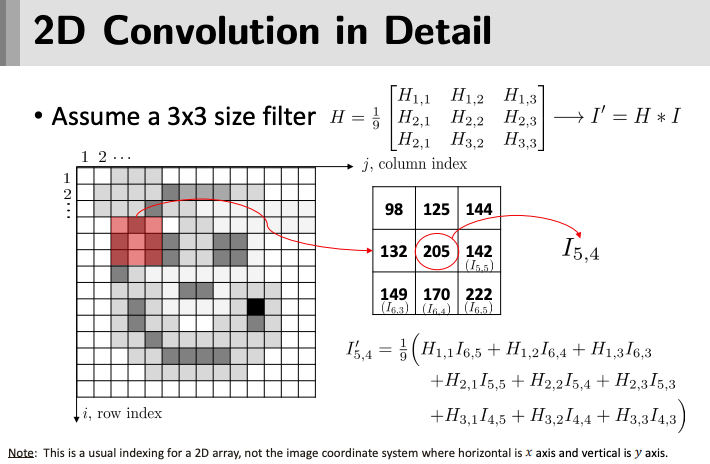
Both correlation and convolution are operations where a kernel (filter) is moved over the image and combines neighboring pixel values.

The correlation of an image $I$ with a kernel $w$ is:

$$I’(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)I(x+s,y+t)$$

The convolution introduces a kernel flip:

$$I’(x,y)=\sum _{s=-a}^a\sum _{t=-b}^{b}w(s,t)I(x-s,y-t)$$

Symmetry: If the kernel is symmetric (e.g., averaging, Gaussian), then flipping it does nothing.

Properties of Convolution

1. Associativity: we can apply filters in any grouping

$$(w\ast v)\ast I=w\ast (v\ast I)$$

2. Commutativity: the order of filters does not matter.

$$(w\ast I)\ast v=(I\ast v)\ast w$$

Kernel Size and Filter design

The kernel $w$ has $mn$ coefficients, where $m=2a+1$ and $n=2b+1$. Designing an image filter is essentially to determine these coefficients.