Method of Finite Differences

Using this example problem:

BVP Example

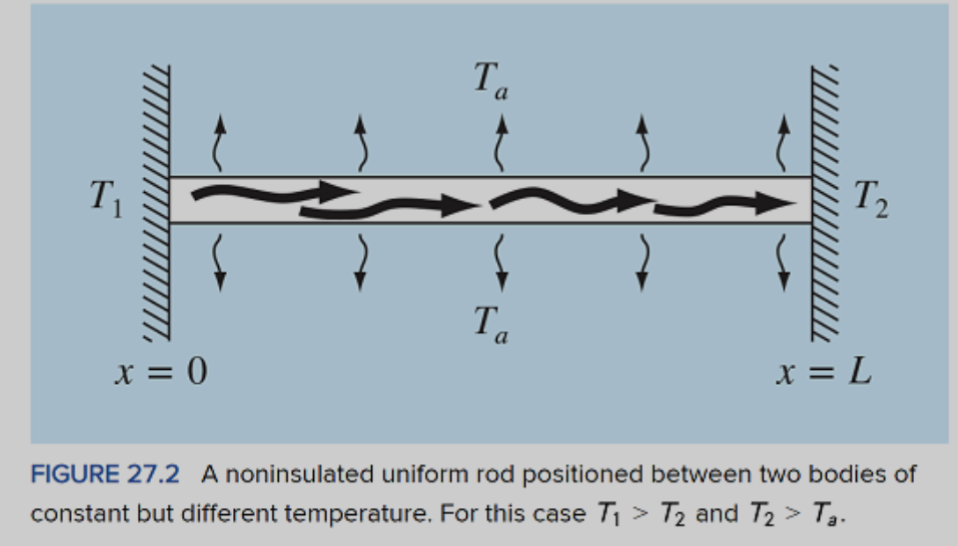
Heat transfer from an uninsulated rod to ambient, with two thermal boundary conditions (one at each end of the rod):

$$\frac{d^{2}T}{d{x}^2}+h^{\prime }(T_a-T)=0$$

With conditions:

$$\begin{array}{r}T(0)=T_1\\ T(L)=T_2\end{array}$$

For $0\le x\le L$, $L=10\text{ m}$:

• $T_a=20$
• $T_1=40$
• $T_2=200$
• $h^{\prime }=0.01$ (Heat coefficient, not step size)

Link to original

The finite difference method uses difference approximation for derivatives to generate a set of equations. For our equation for the example above:

$$\frac{d^{2}T}{d{x}^2}+h^{\prime }(T_a-T)=0$$

Recall for second derivative, centered difference can be written as:

$$f^{\prime \prime }(x_i)=\frac{f(x_{i+1})-2f(x_i)+f(x_i-1)}{h^2}$$

Consider the finite divided difference approximation for the second derivative:

$$\frac{d^{2}T}{d{x}^2}=\frac{T_{i+1}-2T_i+T_{i-1}}{\Delta x^2}$$

Substituting:

$$\frac{T_{i+1}-2T_i+T_{i-1}}{\Delta x^2}-h^{\prime }(T_i-T_a)=0$$

And collecting terms:

$$-T_{i-1}+(2+h^{\prime }\Delta x^2)T_i-T_{i+1}=h^{\prime }\Delta x^2{T}_a$$

Now we can solve this. Using a step size of 2, we have:

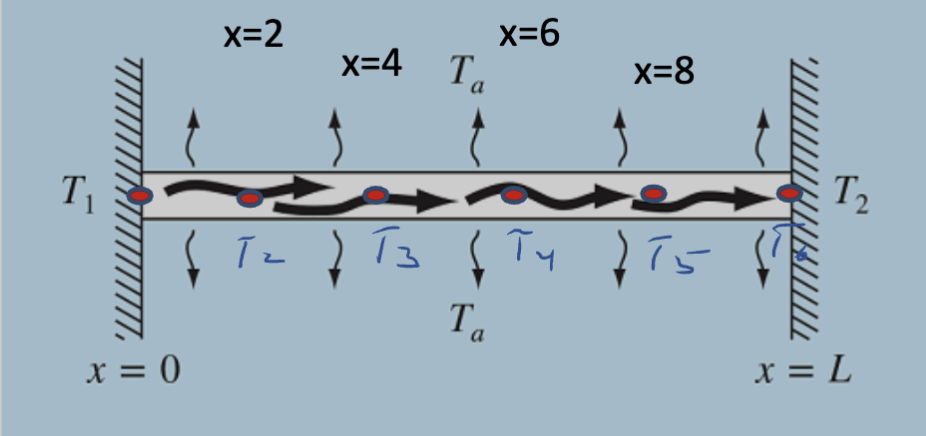
This gives us 4 interior nodes, such that:

$$\left[\begin{array}{cccc}2.04& -1& 0& 0\\ -1& 2.04& -1& 0\\ 0& -1& 2.04& -1\\ 0& 0& -1& 2.04\end{array}\right]\left\{\begin{array}{c}{T}_2\\ T_3\\ T_4\\ T_5\end{array}\right\}=\left\{\begin{array}{c}40.8\\ 0.8\\ 0.8\\ 200.8\end{array}\right\}$$

Using a method such as Gauss-Seidel, this solves to:

$$\begin{array}{rl}{T}_2& =65.9198\\ T_3& =93.7785\\ T_4& =124.5382\\ T_5& =159.4795\end{array}$$

Discretization Concept

The concept behind FDM is to discretize complex geometries. For example, a fixed grid form:

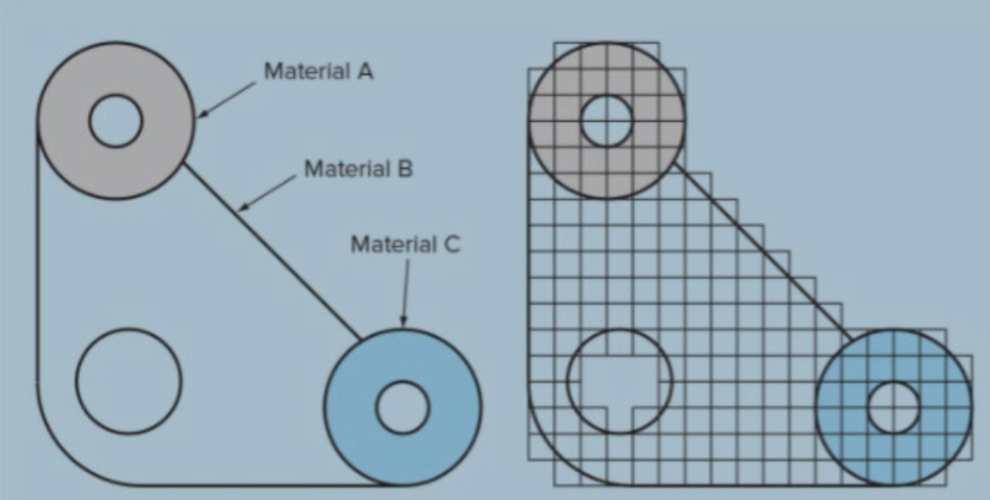
This lets us calculate values at discrete points.

Limitations:

• Challenging to apply FDM to irregular or complex geometries.
• Difficult to address unusual or complex boundary conditions.
• Does not easily address different materials in the same analysis.