Camera Basics

2D image sensors:

• Monocular vision: black/white, e.g. 512x512
• Color: 3 sets of 2D matrix data for RGB, e.g. 512x512x3
• Bit depth: data size of each pixel (e.g. 8 bit: 0 ~ 255)

Image Coordinates (MATLAB)

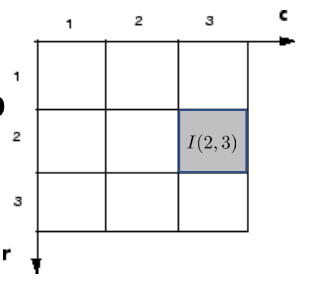
Pixel indices:

• Row and column indices are ordered from top to bottom, and from left to right.
• In general, there are three indices $I({\text{r}}_{\text{ow}},{\text{c}}_{\text{column}},{\text{ch}}_{\text{annel}})$ with ${\text{ch}}_{\text{annel}}\in \{R,G,B\}$.

Spatial coordinates:

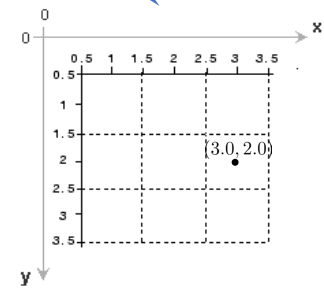
• Intrinsic coordinate: Representing locations in image on a continuous plane
• World coordinate (mapping the intrinsic coordinate to the spatial frame of reference)

Camera Optics

A thin lens with focal length $f$ forms a sharp image of an object at distance $z$ from the lens on an image plane located at distance $e$ behind the lens:

$$\frac{1}{f}=\frac{1}{z}+\frac{1}{e}$$

When the object is far away ($z\to \infty$), the image forms at the focal plane ($e\to f$).

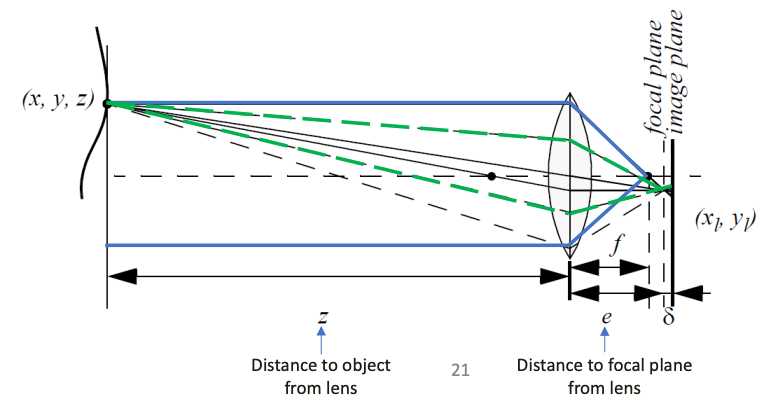
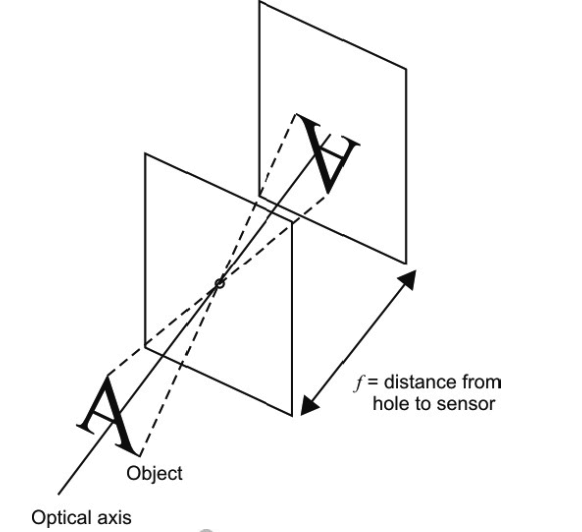
If we let the aperture shrink to a point (or equivalently consider very distant scenes with $z\to \infty$), we obtain the pinhole camera: all rays from a scene point pass through a single point (the optical center) and intersect a plane at distance $f$. This “ray-through-a-point” geometry is the basis for the projection equations below.

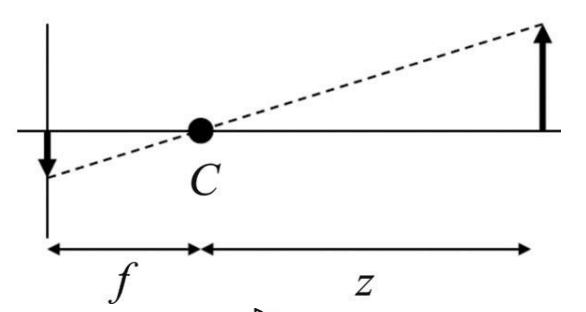
Pinhole Camera Model

Consider a point in camera coordinates $(x,y,z)$ with the origin at the pinhole and $z$ axis pointing forward. Its image coordinates (in metric measurements, not pixel measurements) on a image plane at distance $f$ are $(u,v)$. Similar triangles give us:

$$\frac{u}{x}=\frac{u}{y}=\frac{f}{z}⟹u=\frac{f}{z}x,v=\frac{f}{z}y$$

The division by $z$ is a hallmark of perspective projection; points further away (large $z$) appear closer to the principal point (center of the image from the camera’s geometric perspective).

We can represent the above with a homogeneous representation:

$$\lambda \overline{p}=KP$$

where

$$\overline{p}=\left[\begin{array}{c}u\\ v\\ 1\end{array}\right],K=\left[\begin{array}{ccc}f& 0& 0\\ 0& f& 0\\ 0& 0& 1\end{array}\right],P=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$$

where $\lambda =z$ is the unknown projective scale.

In practice, 3D points are given in a world frame $(x^w,y^w,z^w)$. The rigid motion from world to camera coordinates is:

$$p_c=R{p}_w+t$$

with rotation matrix $R\in \text{SO}(3)$ and translation $t\in {\mathbb{R}}^3$.

In homogeneous form, we can then transform between the two as

$$P=\left[\begin{array}{c}{R}_w^c|t_w^c\end{array}\right]{\bar{P}}^w$$

where $\bar{P}=[x_w{y}_w{z}_{w}1{]}^T$. We call $[R_w^c|t_w^c]$ the extrinsic matrix; it positions the camera within the world.

Real sensors measure pixels, not metric lengths. We let:

• $k_u$ and $k_v$ be the pixel densities (pixels/meter) along the sensor’s $u$ and $v$ axes.
• $(u_0,v_0)$ be the principal point (the pixel where the optical axis hits the sensor, typically near the image center)

Converting the metric projection to pixels gives:

$$u=k_u\frac{f}{z}x+u_0,v=k_v\frac{f}{z}y+v_0$$

• ${\alpha }_u=f{k}_u$ and ${\alpha }_v$ are called the focal lengths in pixels.

Then, the intrinsic calibration matrix that maps metric image-plane coordinates into pixel coordinates is:

$$K=\left[\begin{array}{ccc}{\alpha }_u& 0& u_0\\ 0& {\alpha }_v& v_0\\ 0& 0& 1\end{array}\right]$$

• The image plane is is the surface where the 3D world is projected to form a 2D image

Putting the pieces together, a world point ${\bar{P}}^w=[x_w{y}_w{z}_{w}1{]}^T$ projects to image pixels via

$$\lambda \overline{p}=K\left[\begin{array}{c}{R}_w^c|t_w^c\end{array}\right]{\bar{P}}^w$$