3D Angular Velocities

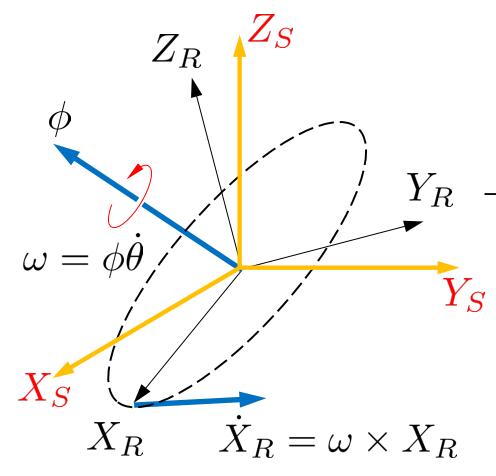
Consider a frame $\{R\}$ rotating with a fixed frame $\{S\}$. For rotational axis $\varphi \in {\mathbb{R}}^3$ and angle $\theta$, we have

$$\begin{array}{r}{\dot{X}}_R=\omega \times X_R\\ {\dot{Y}}_R=\omega \times Y_R\\ {\dot{Z}}_R=\omega \times Z_R\end{array}$$

Noting the relation between $\{R\}$ and $\{S\}$ as $p^s=R_r^s{p}_r$, we can see $r_1$, the first column of $R$, is the coordinates of the unit vector on $X_R$ written with respect to $\{S\}$, and so are $r_2$ and $r_3$ for $Y_R$ and $Z_R$, respectively.

Hence, we have

$${\dot{r}}_i,{\omega }^s\times r_i,i=1,2,3$$

And thus:

$$\dot{R}=\left[\begin{array}{ccc}{\omega }^s\times r_1& {\omega }^s\times r_2& {\omega }^s\times r_3\end{array}\right]={\hat{\omega }}^{s}R$$

where

$$\hat{\omega }=\left[\begin{array}{ccc}0& -{\omega }_3& {\omega }_2\\ {\omega }_3& 0& -{\omega }_1\\ -{\omega }_2& {\omega }_1& 0\end{array}\right]⟹\hat{\omega }=\dot{R}{R}^T$$

We call $\hat{\omega }\in so(3)$, the Lie Algebra of $SO(3)$.