Couette Flow

Couette flow involves steady, incompressible flow between two parallel plates, where the flow is induced by the motion of the upper plate.

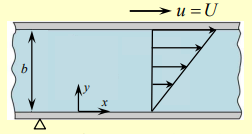
• Two infinite plates are placed at $y=0$ and $y=b$
• The bottom plate is stationary, while the top plate moves with velocity $u=U$ in the x-direction
• Fluid is sheared due to the motion of the upper plate

The continuity equation for incompressible fluids gives us

$$\begin{array}{rl}\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}& =0\\ \frac{\partial u}{\partial x}& =0\\ \therefore u& =u(y)\end{array}$$

The Navier-Stokes Equations give us

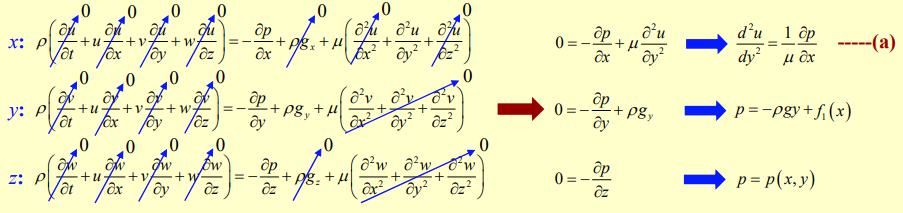
Solving the ODE from the $x$-component by integrating:

$$\begin{array}{rl}\frac{d^{2}u}{d{y}^2}& =\frac{1}{\mu }\frac{dp}{dx}\\ \frac{du}{dy}& =\frac{1}{\mu }\frac{dp}{dx}y+C_1\\ u(y)& =\frac{1}{2\mu }\frac{dp}{dx}{y}^2+C_{1}y+C_2\end{array}$$

We can solve for the constants by applying the stick/no-slip boundary conditions.

At $y=0,u=0$:

$$u(0)=0⟹C_2=0$$

At $y=b,u=U$:

$$U=\frac{1}{2\mu }\frac{dp}{dx}{b}^2+C_{1}b⟹C_1=\frac{U}{b}-\frac{1}{2\mu }\frac{dp}{dx}b$$

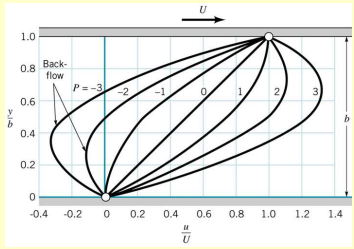
Thus, we finally get:

$$u(y)=\frac{U}{b}y+\frac{1}{2\mu }\frac{dp}{dx}(y^2-by)$$

Alternatively we can write

$$\frac{u}{U}=\frac{y}{b}+P\cdot \frac{y}{b}\left(1-\frac{y}{b}\right)\text{where}P=-\frac{b^2}{2\mu U}\frac{dp}{dx}$$

This is a superposition of:

• A linear shear profile due to the moving plate
• A parabolic pressure-driven profile (like in plane Poiseuille Flow)

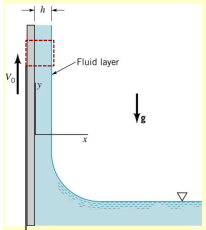
Example: Gravity-Driven Film Flow on a Vertical Wall

This example focuses on a thin fluid film flowing down a vertical wall under gravity. It’s a viscous, incompressible, laminar flow and assumes steady-state conditions. Our goal is to find the average velocity $\overline{V}$.

We also know that since $u=0,v=v,w=0$, the continuity equation for incompressible fluids gives:

$$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0⟹\frac{\partial v}{\partial y}=0⟹v=v(x)$$

Also, the pressure is constant across the free surface $p=p(y)$:

The Navier-Stokes equations give:

Integrating the $y$-component to find the velocity profile:

$$\begin{array}{rl}0& =-\rho g+\mu \frac{d^{2}v}{d{x}^2}\\ \frac{d^{2}v}{d{x}^2}& =\frac{\gamma }{\mu }\\ v(x)& =\frac{\gamma }{2\mu }{x}^2+C_{1}x+C_2\end{array}$$

We can use boundary conditions to solve for the constants.

• At the wall $x=0$, we have the no-slip condition such that $v=V_0$:

$$v=V_0⟹C_2=V_0$$

• At the free surface $x=h$, we have $v=0$:

$$\frac{dv}{dx}=0⟹C_1=-\frac{\gamma h}{\mu }$$

Thus, the final velocity profile is:

$$v={\frac{\gamma }{2\mu }}^2-\frac{\gamma h}{\mu }x+V_0$$

The volumetric flow rate:

$$\begin{array}{rl}q& ={\int }_0^{h}v(x)dx=V_{0}h-\frac{\gamma h^3}{3\mu }=\overline{V}h\\ \bar{v}& =\frac{q}{h}=V_0-\frac{\gamma h^2}{3\mu }\end{array}$$