In Poiseuille flow, we have steady, axisymmetric flow of a viscous, incompressible fluid through a long, straight pipe of circular cross-section (radius ).
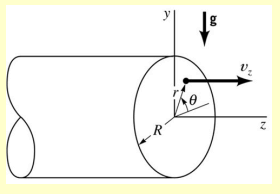
In this case, we use cylindrical coordinates. We assume:
The continuity equation for incompressible fluids in cylindrical coordinates reduces to:
Given our assumptions, this becomes
Applying the Navier-Stokes in cylindrical coordinates:
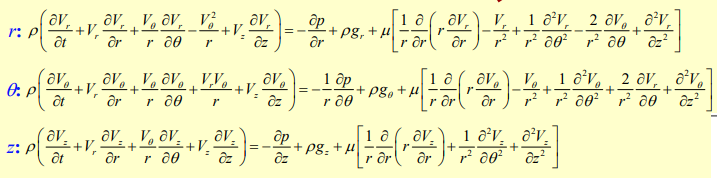
The -direction gives:
The -direction gives:
Thus, in general we have
The -direction (axial) gives:
Solving the axial momentum equation gives:
Boundary conditions:
- No-slip at the wall: at gives
- Velocity finite at centerline: finite as gives
Thus, we have:
Volumetric flow rate:
If the pressure drop over length is , then
Substituting into the equation for :
which is called Poiseuille’s Law.