Differential Form of Conservation of Mass

Recall the continuity equation based on the conservation of mass:

$$\frac{\partial }{\partial t}{\int }_{\text{C.V.}}\rho d\forall +{\int }_{\text{C.S.}}\rho \mathbf{V}\cdot \text{n}dA=0$$

To derive a differential form, consider the fluid element as a small cube with sides $dx,dy,dz$.

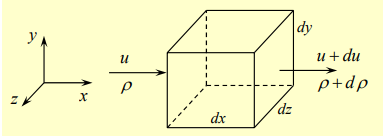
Pressure inside the element is constant. Since the element is small, the volume integral in the continuity equation can be written as

$$\frac{\partial }{\partial t}{\int }_{\text{cv}}\rho d\forall =\frac{\partial \rho }{\partial t}dxdydz$$

Let’s consider the second term of the continuity equation describing mass flow rate. Let’s start with the $x$ direction.

Inflow to the left face is given as:

$$\rho uA=\rho udydz$$

Outflow from the right face is:

$$(\rho +d\rho )(u+du)A=(\rho u+\rho du+ud\rho +dud\rho )dy$$

The net mass flowrate is then:

$$(\rho du+ud\rho )dydz=d(\rho u)dydz=\frac{\partial (\rho u)}{\partial x}dxdydz$$

Similarly, in the $y$ and $z$ directions, we have

$$\frac{\partial (\rho v)}{\partial y}dxdydz,\frac{\partial (\rho w)}{\partial z}dzdydz$$

Combining all three directions and substituting back into the continuity equation gives us:

$$\left[\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}+\frac{\partial (\rho w)}{\partial z}\right]dxdydz+\frac{\partial \rho }{\partial t}dxdydz=0$$

or simply

$$\begin{array}{rl}\frac{\partial \rho }{\partial t}+\frac{\partial (\rho u)}{\partial x}+\frac{\partial (\rho v)}{\partial y}+\frac{\partial (\rho w)}{\partial z}& =0\\ \frac{\partial \rho }{\partial t}+\nabla \cdot \rho \mathbf{V}& =0\end{array}$$

For steady flows:

$$\nabla \cdot \rho V=0$$

For incompressible flows:

$$\begin{array}{r}\nabla \cdot \mathbf{V}=0⟹\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\end{array}$$

Example

Given:

$$\begin{array}{rl}u& =x^2+y^2+z^2\\ v& =xy+yz+z\end{array}$$

Determine $w$ if the flow is incompressible.

For incompressible flows, we have:

$$\begin{array}{r}\nabla \cdot \mathbf{V}=0⟹\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0\end{array}$$

Then:

$$\begin{array}{rl}\frac{\partial u}{\partial x}& =2x\\ \frac{\partial v}{\partial y}& =x+z\\ \frac{\partial w}{\partial z}& =-3x-z\end{array}$$

Integrating:

$$w=-3xz-\frac{1}{2}{z}^2+f(x,y)$$