Dominant Poles and Zeros

We can define dominant and non-dominant poles/zeros based on their locaiton in the complex $s$-plane:

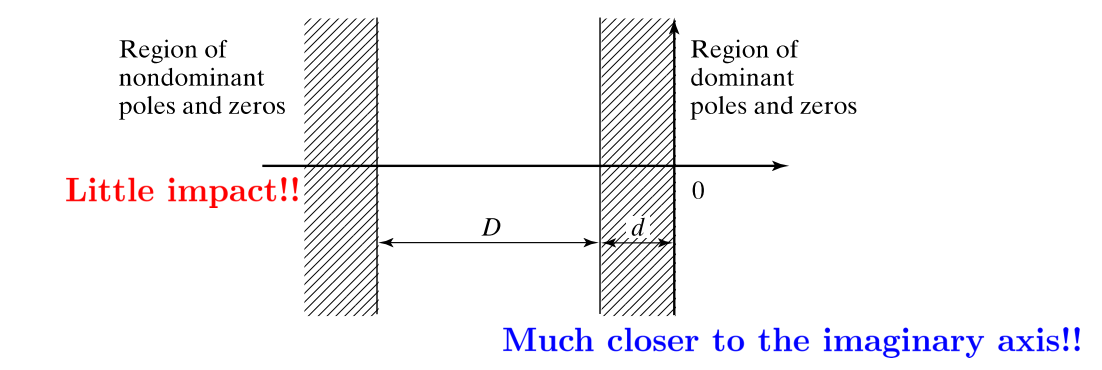
Dominant poles/zeros are closer to the imaginary axis, meaning they decay slowly and strongly influence the system’s long-term behavior.

Nondominant poles/zeros are further left (larger negative real part), so they decay quickly and have little on long-term dynamics.

Typically $\frac{D}{d}>5\sim 10$ constitutes a dominant vs. imaginary poles.

Examples

A unity feedback system with the loop transfer function:

$$L(s)=\frac{10(s+10)}{s(s+3)(s+5)}$$

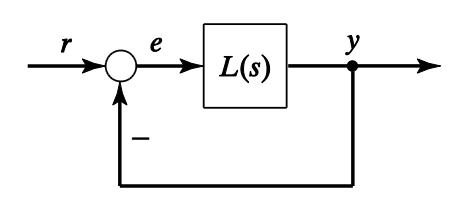
The closed-loop transfer function from $r(t)$ to $y(t)$ is given by

$$T(s)=\frac{L(s)}{1+L(s)}=\frac{10(s+10)}{(s+6.5182)[(s+0.7409{)}^2+3.8461^2]}$$

• One zero at $s=-10$ (Green)
• One real pole at $s=-6.5182$ (Blue)
  • Non-dominant because far away from imaginary axis
• Complex conjugate pole pair at $s=-0.7409\pm j3.8461$ (Red)
  • Dominant (close to imaginary axis)

The system performance can be extimated ont he basis of the pair of poles.

$$\begin{array}{rl}T(s)& \approx \frac{10\times 10}{6.5182[(s+0.7409{)}^2+3.8461^2]}\\ & =\frac{3.9168^2}{s^2+2\times 0.189\times 3.9168s+3.9168s}\end{array}$$

This matches the standard second-order form of

$$T(s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$

From this:

• Natural frequency ${\omega }_n=3.9168$
• Damping ratio $\zeta =0.189$

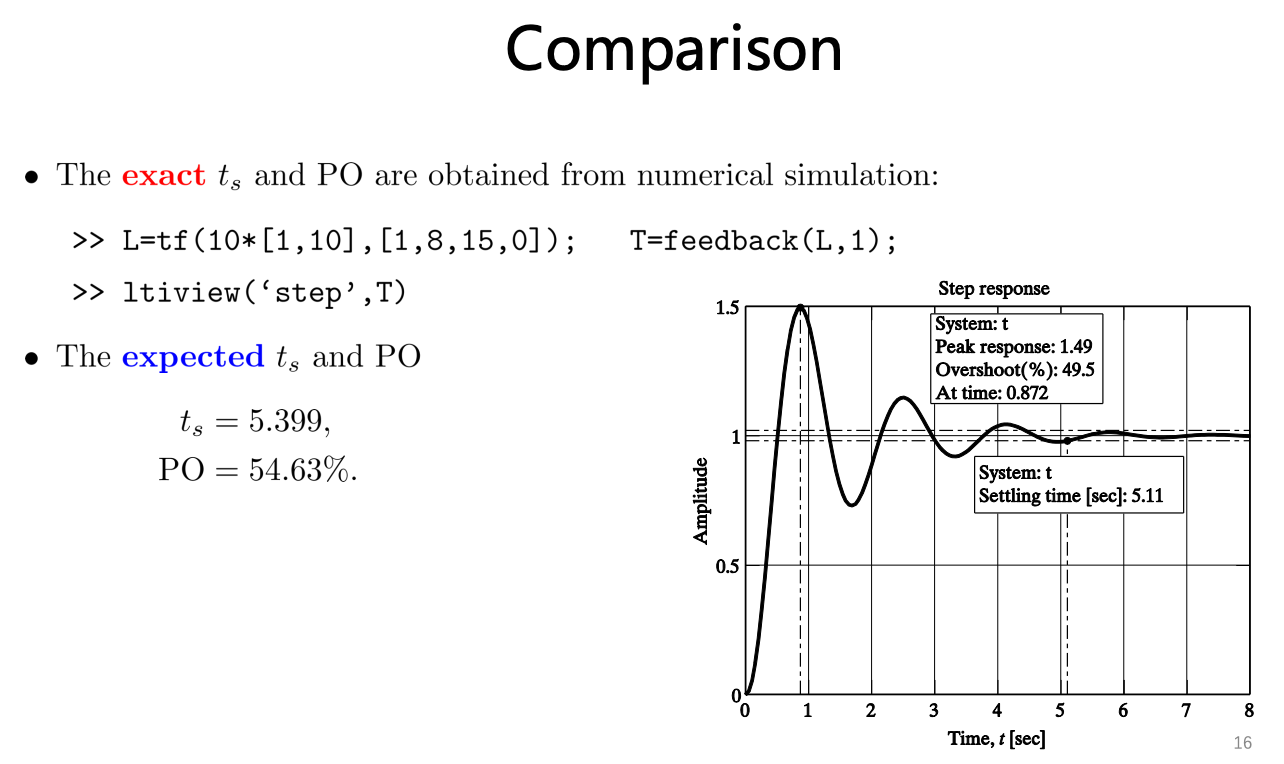
Thus, the expected step response will be:

$$t_s=\frac{4}{\zeta {\omega }_n}=5.399(\text{2\% tolerance})$$

and

$$\text{PO}=e^{\frac{-\zeta \pi }{\sqrt{1-{\zeta }^2}}}\times 100\%=54.63\%$$