Advanced Root Locus Example

Let’s consider

$$L(s)=\frac{s+1}{s(s+2)((s+1{)}^2+1)}$$

Rule A:

$$\{\begin{array}{l}m=1\\ n=4\end{array}⟹4\text{ branches}$$

Rule B: Branches start at open-loop poles:

$$s=0,s=-2,s=-1\pm j$$

Rule C: Branches end at open-loop zeros:

$$s=-1,\pm \infty$$

To determine which portions of the real axis lie of the root locus, we try a test point.

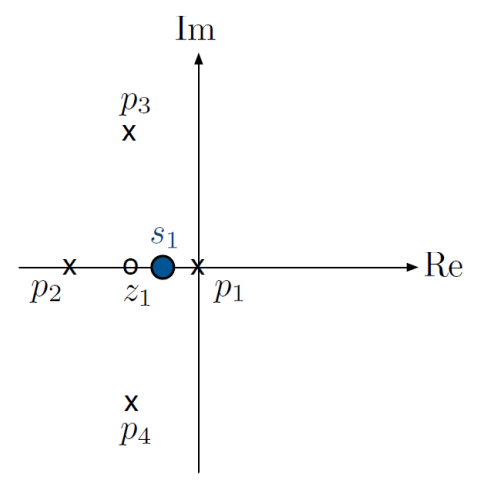
We can calculate the angles from $s_1$ to each zero and pole to determine if satisfies the pole condition.

$$\begin{array}{rl}\angle (s_1-z_1)& =0°(s_1>z_1)\\ \angle (s_1-p_1)& =180°(s_1<p_1)\\ \angle (s_1-p_2)& =0°(s_1<p_2)\\ \angle (s_1-p_3)& =-\angle (s_1-p_4)\end{array}$$

We have

$$\begin{array}{rl}& \angle (s_1-z_1-[\angle (s_1-p_1)+\angle (s_1-p_2)+\angle (s_1-p_3)+\angle (s_1-p_4)])\\ & =0°-[180°+0°+0°]=-180°\end{array}$$

We can try another test point:

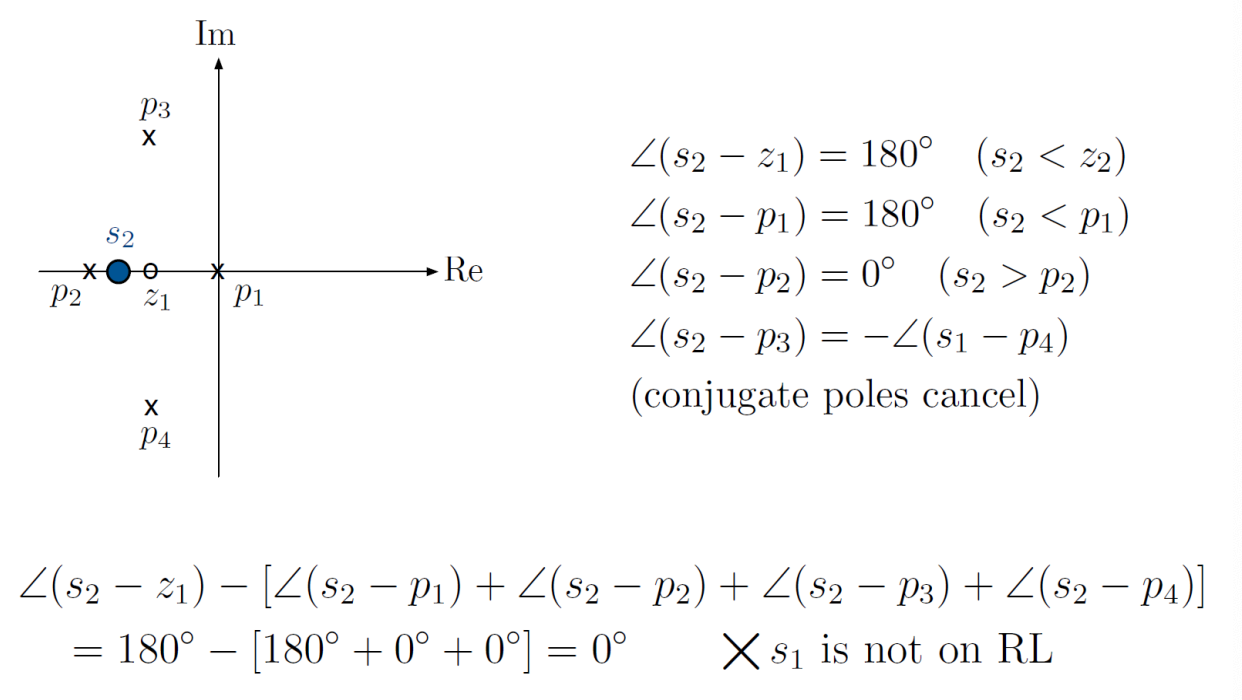
We can shorten this process by using Rule D:

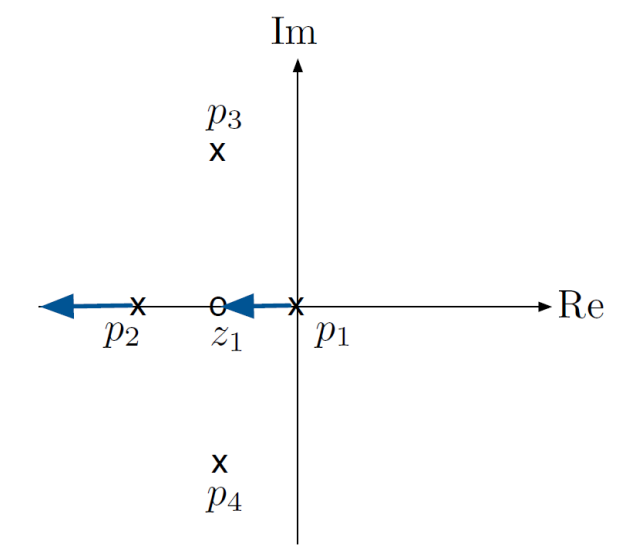
Rule E:

$$\angle s=\frac{(2\ell +1)\cdot 180°}{3},\ell =0,1,2$$

Then:

$$\begin{array}{rl}\ell =0& :\frac{2\cdot 0+1}{3}180°=60°\\ \ell =1& :\frac{2\cdot 1+1}{3}180°=180°\\ \ell =2& :\frac{2\cdot 2+1}{3}180°=\frac{5}{3}180°=\left(2-\frac{1}{3}\right)180°=-60°\end{array}$$

Thus, the asymptotes have angles $60°,180°,-60°$.

For rule F, we see that the characteristic polynomial for our system is:

$$s^4+4s^3+6s^2+(4+K)s+K$$

The Routh array:

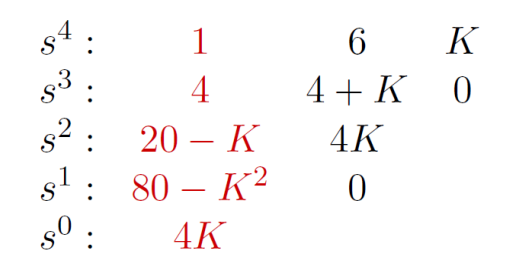
For stability, we need $20-K>0$, $80-K^2>0$, $4K>0$. Combining these, we see that the characteristic polynomial is stable for $K<\sqrt{80}=4\sqrt{5}$.

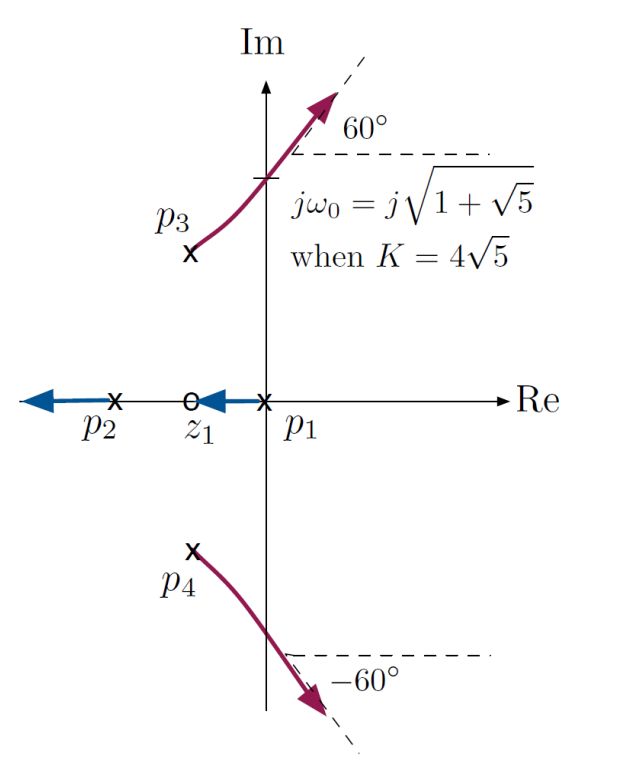
To find the $j\omega$ crossing, plug in and solve:

$$\begin{array}{r}(j\omega {)}^4+4(j\omega {)}^3+6(j\omega {)}^2+(4+4\sqrt{5})j\omega +4\sqrt{5}=0\\ {\omega }^4-4j{\omega }^3-6{\omega }^2+(4+4\sqrt{5})j\omega +4\sqrt{5}=0\end{array}$$

• Real part: ${\omega }^4-6{\omega }^2+4\sqrt{5}=0$
• Imaginary part: $-4{\omega }^3+4(1+\sqrt{5})\omega =0$, which gives ${\omega }^2=1+\sqrt{5}$.

Thus, we have $j\omega$-crossing at $j{\omega }_0=\sqrt{1+\sqrt{5}}\approx 1.8$, when $K=4\sqrt{5}\approx 8.9$.