Additional Poles and Zeroes

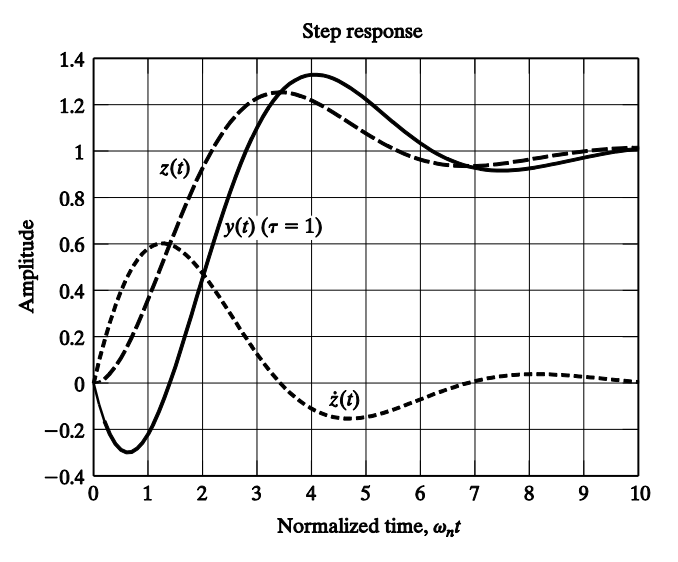
Most systems can be better modeled using high-order transfer functions (more than 2 poles) and have finite zeros. How do these additional poles and zeros affect the standard system response?

Additional Pole

Consider the case when a pole is added to a standard second-order underdamped system:

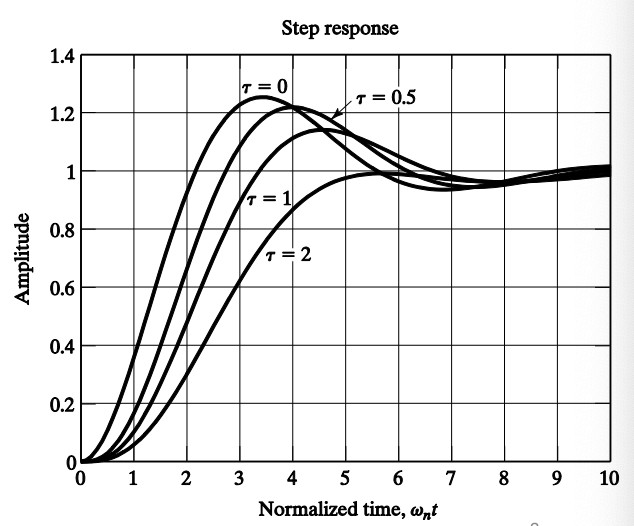
The response of this system will be slower and smoother than the response of the standard second-order system.

• Additional low-pass filtering

Effects of a pole on step response with $\zeta =0.4$:

Additional Zero

Minimum Phase Zero

Consider the case when a zero is added to a standard second-order underdamped system, where the the zero added is a minimum phase zero ($\text{Re}(z)<0$).

It’s easy to see that:

$$y(t)=z(t)+\frac{\tau }{{\omega }_n}\dot{z}(t)$$

Since $\dot{z}(t)>0$ for $t<t_p$, the system will have a shorter rise time, a shorter peak time, and a larger overshoot.

Effect of a minimum phase zero on step response:

Nonminimum Phase Zero

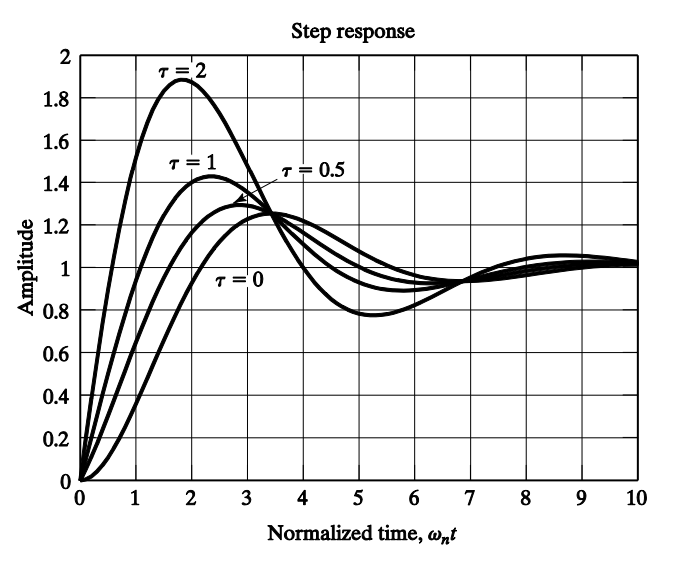
Assume the zero added is a nonminimum phase zero ($\text{Re}(z)>0$).

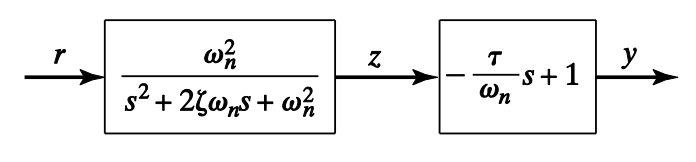
Then we have:

$$y(t)=z(t)-\frac{\tau }{{\omega }_n}\dot{z}(t)$$

Since $\dot{z}(t)>0$ for $t<t_p$, the response shows undershoot behavior, which is undesirable.

Effects of a nonminimum phase zero on step response with $\zeta =0.4$: