Rayleigh's Method

We can use the principle of conservation to obtain the natural frequency of a mass-spring system if the spring is linear. This can be useful because we don’t need to find the equation of motion first.

In simple harmonic motion, the kinetic energy is maximum and the potential energy is minimum at the equilibrium position $x=0$. When the displacement is maximum, the the potential energy is maximum but the kinetic energy is zero. Thus, we have:

$${\text{PE}}_{\text{max}}+{\text{KE}}_{\text{min}}={\text{PE}}_{\text{min}}+{\text{KE}}_{\text{max}}$$

Simple harmonic motion

$$\begin{array}{rl}x(t)& =A\sin ({\omega }_{n}t+\varphi )\\ A& =\sqrt{x^2(0)+{\left[\frac{\dot{x}(0)}{{\omega }_n}\right]}^2}\\ \sin \varphi & =\frac{x(0)}{A},\cos \varphi =\frac{\dot{x}(0)}{A}\\ \dot{x}(t)& =A{\omega }_n\cos ({\omega }_{n}t+\varphi )=A{\omega }_n\sin \left({\omega }_{n}t+\varphi +\frac{\pi }{2}\right)\\ \ddot{x}(t)& =A{\omega }_n^2\sin ({\omega }_{n}t+\varphi )=A{\omega }_n^2\sin ({\omega }_{n}t+\varphi +\pi )\end{array}$$

Example

Using Rayleigh’s method, find the natural frequency of this system. Assume no slip.

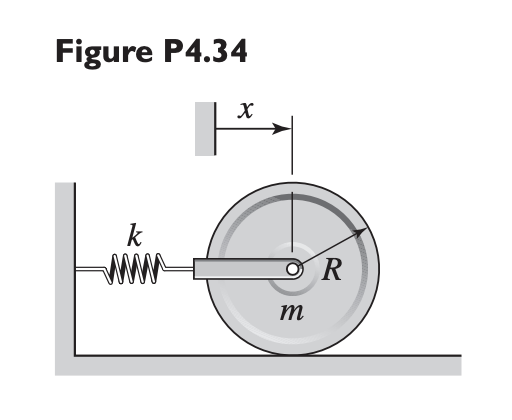
Recall that for a mass-spring system:

$$\begin{array}{rl}{\omega }_n^2& =\frac{k}{m}\\ {\omega }_n& =\sqrt{\frac{k}{m}}\\ 2\pi f_n& =\sqrt{\frac{k}{m}}\\ f_n& =\frac{1}{2\pi }\sqrt{\frac{k}{m}}\end{array}$$

To solve the problem, we need to find the equivalent mass and equivalent stiffness, and take:

$${\omega }_n=\sqrt{\frac{k_{\text{eq}}}{k_{\text{eq}}}}$$

For kinetic energy, we have:

$$\text{KE}=\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}I{\omega }^2$$

where $\omega =\frac{\dot{x}}{R}$ due to the no-slip condition. Thus, we have:

$$\begin{array}{rl}\text{KE}& =\frac{1}{2}m{\dot{x}}^2+\frac{1}{2}\left(\frac{m{R}^2}{2}\right)\left(\frac{{\dot{x}}^2}{R^2}\right)\\ & =\frac{3}{4}m{\dot{x}}^2\end{array}$$

For potential energy, we simply have:

$$\text{PE}=\frac{1}{2}k{x}^2$$

Rayleigh’s method gives:

$${\text{PE}}_{\text{max}}+{\text{KE}}_{\text{min}}={\text{PE}}_{\text{min}}+{\text{KE}}_{\text{max}}$$

We have ${\text{KE}}_{\text{min}}=0$ when $\dot{x}=0$. We also have ${\text{PE}}_{\text{min}}=0$ when there is no deflection ($x=0$).

Thus, Rayleight’s method simplifies to:

$$\begin{array}{rl}{\text{KE}}_{\text{max}}& ={\text{PE}}_{\text{max}}\\ \frac{3}{4}m{\dot{x}}_{\text{max}}^2& =\frac{1}{2}k{x}_{\text{max}}^2\end{array}$$

Let us define $x_{\text{max}}=A$. Then, we also have:

$${\dot{x}}_{\text{max}}=A{\omega }_n$$

Following this, we have:

$$\begin{array}{rl}\frac{3}{4}m{A}^2{\omega }_n^2& =\frac{1}{2}k{A}^2\\ \frac{3}{4}m{\omega }_n^2& =\frac{1}{2}k\\ {\omega }_n^2& =\frac{1/2}{3/4}\left(\frac{k}{m}\right)\\ {\omega }_n& =\sqrt{\frac{2}{3}\frac{k}{m}}\end{array}$$