Velocity Analysis

Linear velocity:

$$\vec{v}=\frac{dR}{dt}$$

where $R$ is the position.

Angular velocity:

$$\omega =\frac{d\theta }{dt}$$

Types of velocity:

• Absolute velocity: Velocity with respect to a point on the same body fixed at origin of global coordinate axes system.
• Velocity difference: Velocity with respect to a point on the same body that is not fixed

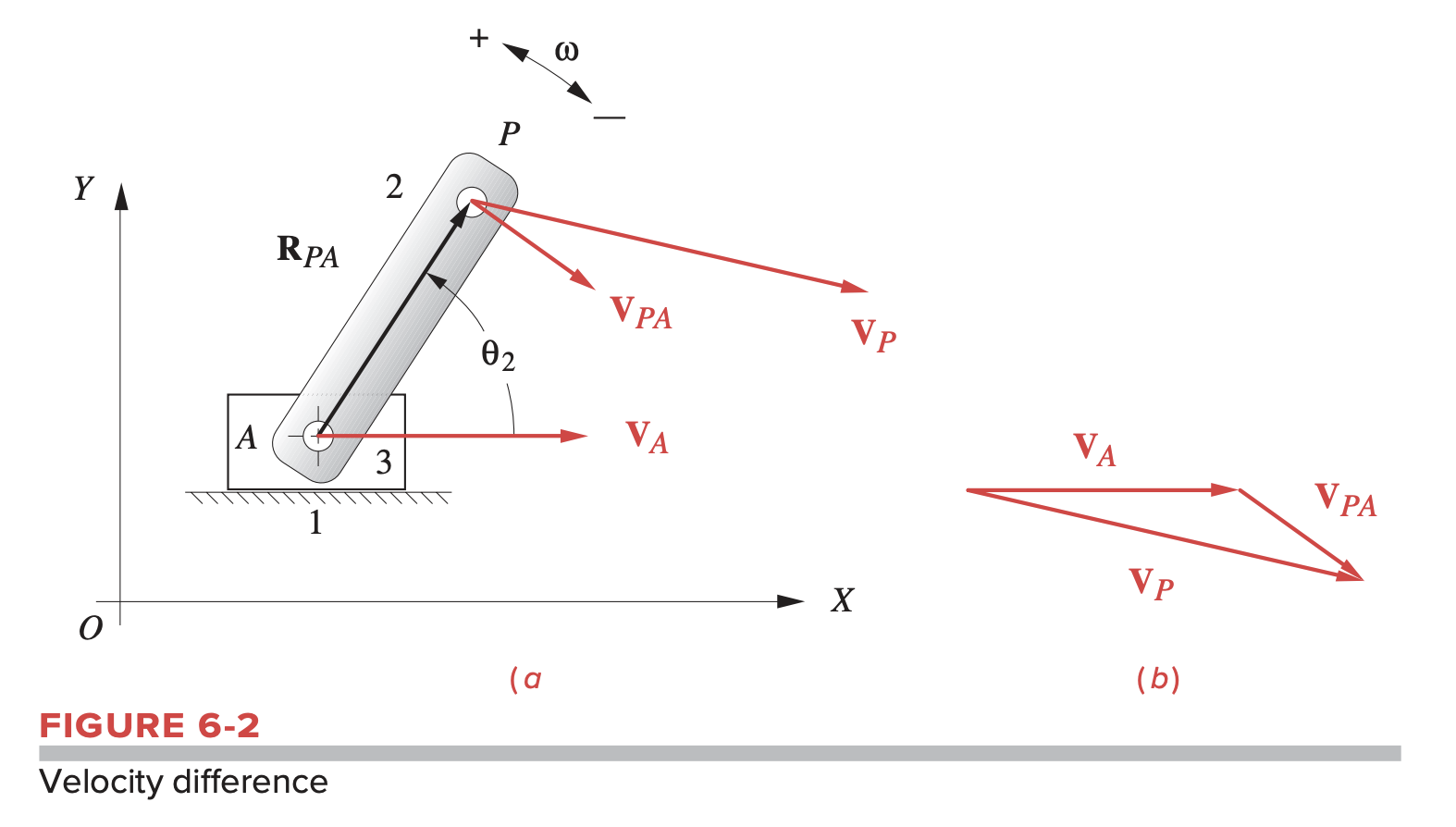
• Relative velocity: Velocity with respect to a point on a different body that is not fixed

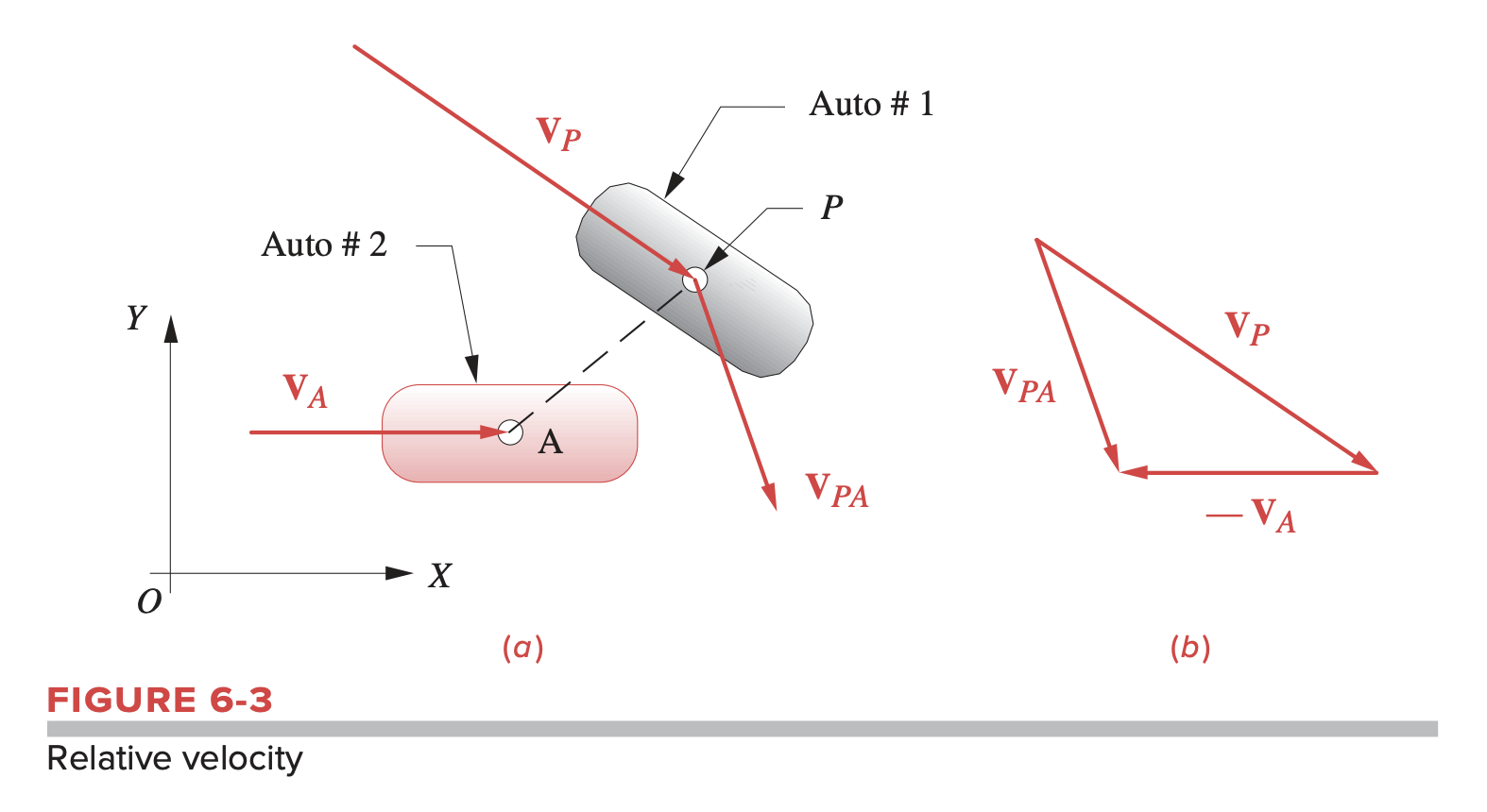
Complex Number Representation

Recall that position is given by:

$$R_{PA}=p{e}^{j\theta }$$

Thus, we have:

$$V_{PA}=\frac{d{R}_{PA}}{dt}=pj{e}^{j\theta }\frac{d\theta }{dt}=p\omega j{e}^{j\theta }$$

where $p$ is the scalar length of vector $R_{PA}$.

Vector Loop Velocity Analysis of Fourbar Linkage

Step 1: Check the reference frame/coordinate system. $R_1$ should be fixed with angle of zero with respect to $x$-axis. If this is not the case, set up a local coordinate system that meets this convention.

Step 2: Check to see if you have all the angles you need. If we are missing ${\theta }_3$, ${\theta }_4$, we will need to do a position analysis first to find these angles.

Step 3: Calculate ${\omega }_3$ and ${\omega }_4$.

To do this, we use the vector-loop position equations for the fourbar pin-jointed linkage, which were derived here. The linkage in Figure 6-20 on which we also show an input angular velocity ${\omega }_2$ applied to link 2. This ${\omega }_2$ can be a time-varying input velocity.

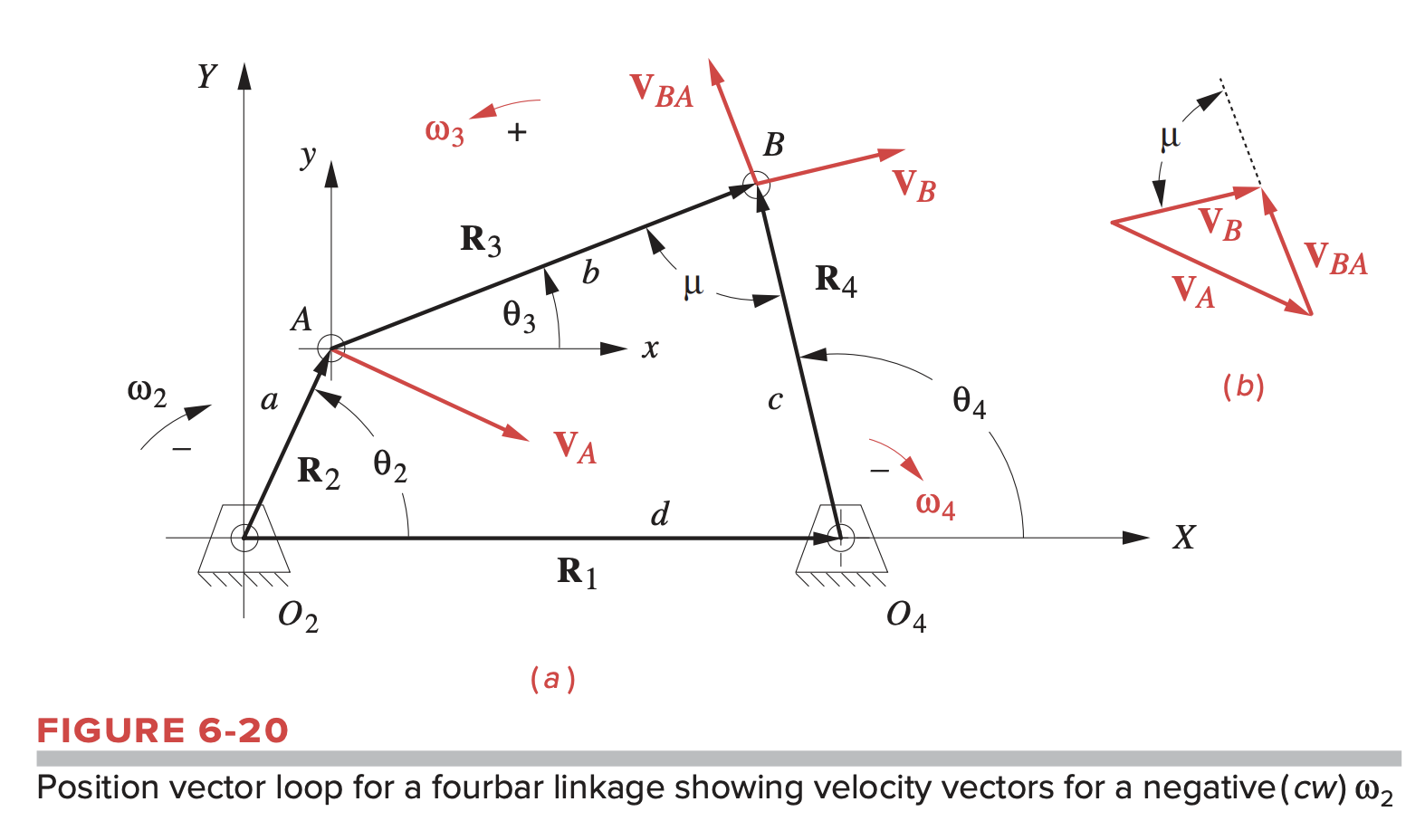
The vector loop equation is:

$$R_2+R_3-R_4-R_1=0$$

which we can substitute the complex number notation for the vectors

$$a{e}^{j{\theta }_2}+b{e}^{j{\theta }_3}-c{e}^{j{\theta }_4}-d{e}^{j{\theta }_1}=0$$

To get an expression for velocity, we can differentiate this with respect to time:

$$\begin{array}{rl}ja{e}^{j{\theta }_2}\frac{d{\theta }_2}{dt}+jb{e}^{j{\theta }_3}\frac{d{\theta }_3}{dt}-jc{e}^{j{\theta }_4}\frac{d{\theta }_4}{dt}& =0\\ ja{\omega }_2{e}^{j{\theta }_2}+jb{\omega }_3{e}^{j{\theta }_3}-jc{\omega }_4{e}^{j{\theta }_4}& =0\end{array}$$

where we take advantage of the fact that ${\omega }_n=\frac{d{\theta }_n}{dt}$. Note that the ${\theta }_1$ term has been dropped, since $d{\theta }_1/dt=0$.

The equation above is also the relative velocity or velocity difference equation:

$$V_A+V_{BA}-V_B=0$$

where:

$$\begin{array}{rl}{V}_A& =ja{\omega }_2{e}^{j{\theta }_2}\\ V_{BA}& =jb{\omega }_3{e}^{j{\theta }_3}\\ V_B& =jc{\omega }_4{e}^{j{\theta }_4}\end{array}$$

Solving $V_A+V_{BA}-V_B=0$ gives:

$$\begin{array}{r}{\omega }_3=\frac{a{\omega }_2}{b}\frac{\sin ({\theta }_4-{\theta }_2)}{\sin ({\theta }_3-{\theta }_4)}\\ {\omega }_4=\frac{a{\omega }_2}{b}\frac{\sin ({\theta }_2-{\theta }_3)}{\sin ({\theta }_4-{\theta }_3)}\end{array}$$

Step 4: Solve for the linear velocities $V_A,V_{BA},V_B$ with:

$$\begin{array}{rl}{V}_A& =ja{\omega }_2(\cos {\theta }_2+j\sin {\theta }_2)=a{\omega }_2(-\sin {\theta }_2+j\cos {\theta }_2)\\ V_{BA}& =jb{\omega }_3(\cos {\theta }_3+j\sin {\theta }_3)=b{\omega }_3(-\sin {\theta }_3+j\cos {\theta }_3)\\ V_B& =jc{\omega }_4(\cos {\theta }_4+j\sin {\theta }_4)=c{\omega }_3(-\sin {\theta }_4+j\cos {\theta }_4)\end{array}$$

If we need to solve for both the open and crossed positions, we will need to do steps 3 and 4 twice; once with ${\theta }_3,{\theta }_4$ for the open position, and once with ${\theta }_3,{\theta }_4$ for the closed position.

Vector Loop Velocity Analysis of Crank-Slider

We can follow a similar approach for a crank-slider system. Crank is input, slider is output.

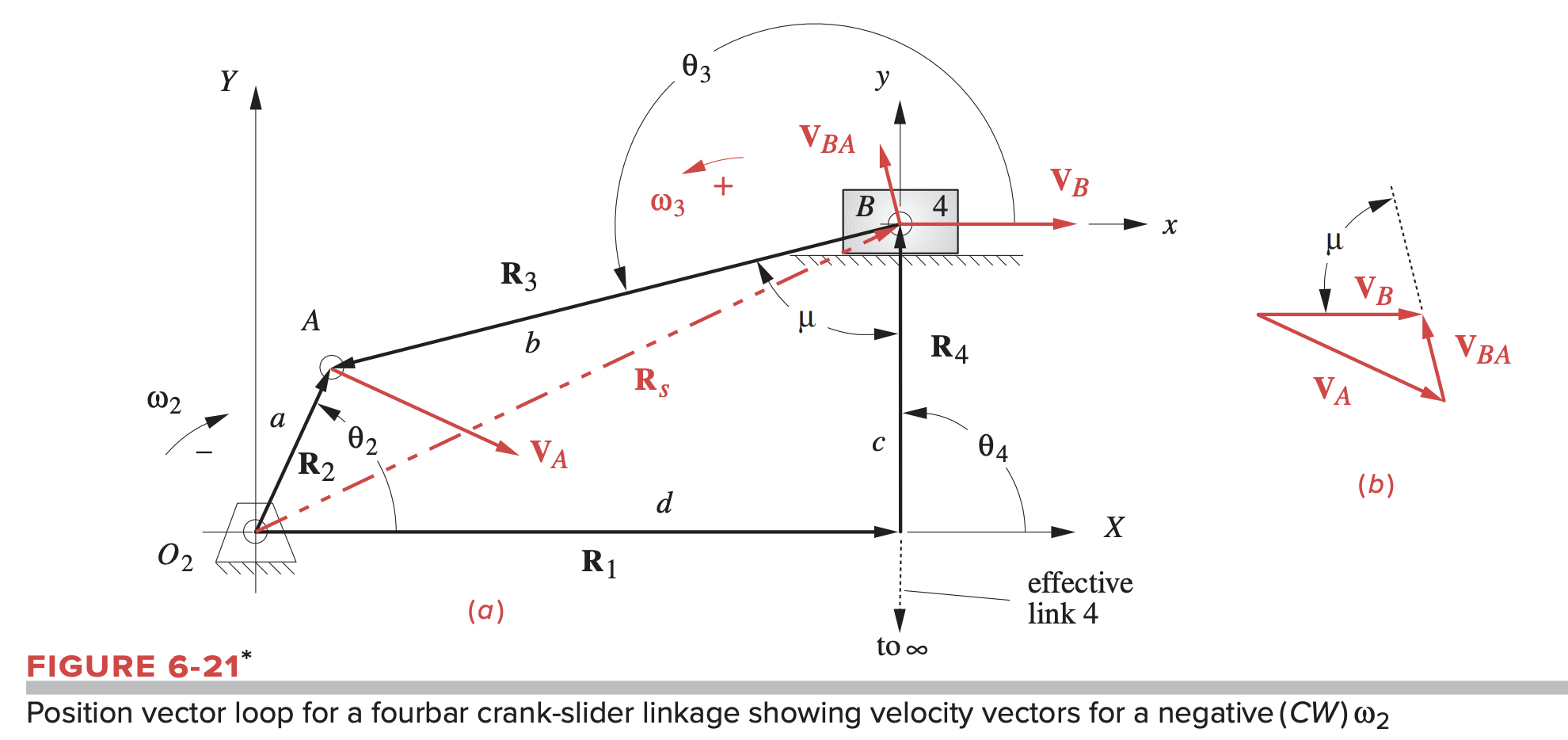
Step 1: Check the reference frame/coordinate system.

Step 2: If we are missing ${\theta }_3$ and $d$ you will need to do a position analysis first to find these parameters.

Step 3: Calculate angular velocity (${\omega }_3$) and linear velocity of slider block $\dot{d}=\frac{d}{dt}(d)$. These can be derived similar to above by writing the vector loop equation and then differentiating with respect to tiem.

We have:

$$\begin{array}{rl}{\omega }_3& =\frac{d{\theta }_3}{dt}=\frac{a}{b}\frac{\cos {\theta }_2}{\cos {\theta }_3}{\omega }_2\\ \dot{d}& =-a{\omega }_2\sin {\theta }_2+b{\omega }_3\sin {\theta }_3\end{array}$$

Step 4: Solve for the linear velocities, $V_A,V_{AB},V_{BA}$:

$$\begin{array}{rl}{V}_A& =a{\omega }_2(-\sin {\theta }_2+j\cos {\theta }_2)\\ V_{AB}& =b{\omega }_3(-\sin teht{a}_3+j\cos {\theta }_3)\\ V_{BA}& =-V_{AB}\end{array}$$

If we need to solve for both the open and crossed positions, we will need to do steps 3 and 4 twice; once with ${\theta }_3,d$ for the open position, and once with ${\theta }_3,d$ for the closed position.