Distortion Energy Theory

The distortion-energy theory predicts that yielding occurs when the distortion strain energy per unit volume reaches or exceeds the distortion strain energy per unit volume for yield in simple tension or compression of the same material.

The distortion-energy (DE) theory originated from the observation that ductile materials stressed hydrostatically (equal principal stresses) exhibited yield strengths greatly in excess of the values given by the simple tension test.

The formula for ${\sigma }_{\text{av}}$ is simply:

$${\sigma }_{\text{av}}=\frac{{\sigma }_1+{\sigma }_2+{\sigma }_2}{3}$$

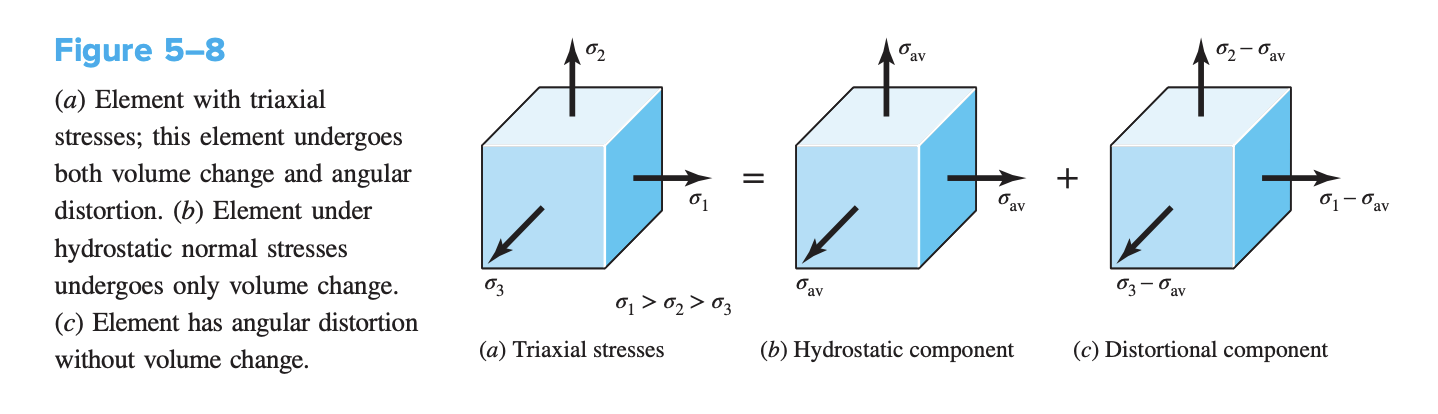
The basic process is to:

• Find equation for strain energy per unit volume ($u$) for a stress element with tri-axial stresses
• Find equation for strain energy per unit volume due to hydrostatic component of tri-axial stresses only ($u_v$)
• Find strain energy per unit volume due to distortion component of tri-axial stresses only by solving for $u-u_v$
• Derive von Mises Stress

General Case

von Mises Stress and yield conditions are given as:

$${\sigma }^{\prime }={\left[\frac{({\sigma }_1-{\sigma }_2{)}^2+({\sigma }_2-{\sigma }_3{)}^2+({\sigma }_3-{\sigma }_1{)}^2}{2}\right]}^{1/2}\ge S_y$$

When designing with a factor of safety $n$:

$${\sigma }^{\prime }=\frac{S_y}{n}$$

Plane Stress

For plane stress, we have two principal stresses in the plane of analysis, such that ${\sigma }_A\ge {\sigma }_B$. The third principal stress is zero. The von Mises stress can be written as:

$${\sigma }^{\prime }=({\sigma }_A^2-{\sigma }_A{\sigma }_B+{\sigma }_B^2{)}^{1/2}$$

which is just the general case equation but with one of the stresses as zero.

This can be visualized as a rotated ellipse on the ${\sigma }_A,{\sigma }_B$ plane:

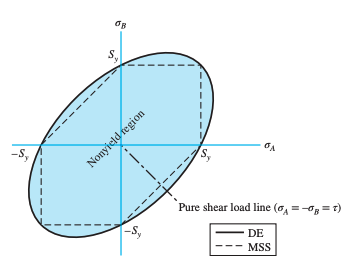
• As can be seen from the graph, DE is less conservative than MSS
  • DE theory: $S_{sy}=0.577S_y$
  • MSS theory: $S_{sy}=0.5S_y$

Shear Stress

For shear stress (pure shear, ${\sigma }_x={\sigma }_y-0$), we have yield conditions such that:

$$\begin{array}{rl}{\sigma }^{\prime }& =(3{\tau }_{xy}^2{)}^{1/2}\ge S_y\\ {\tau }_{xy}& \ge \frac{S_y}{\sqrt{3}}=0.577S_y\end{array}$$

For design:

$${\sigma }^{\prime }={\tau }_{xy}\sqrt{3}=\frac{S_y}{n}$$

Equations in terms of $xyz$

General case/3D:

$${\sigma }^{\prime }=\frac{1}{\sqrt{2}}({\sigma }_x^2-{\sigma }_x{\sigma }_y+{\sigma }_y^2+3{\tau }_{xy}^2{)}^{1/2}$$

The yield condition is unchanged:

$${\sigma }^{\prime }\ge S_y$$

Design is also unchanged:

$${\sigma }^{\prime }=\frac{S_y}{n}$$