Beam Deflection Due to Bending

The curvature of a beam subjected to a bending moment $M$ is given by:

$$\frac{1}{\rho }=\frac{M}{EI}$$

where $\rho$ is the radius of curvature and $I$ is the second moment of area of the beam cross-section. This is relevant for cases where the beam is under transverse loading.

Beam Examples

Cantilever Beam

For example, a cantilever beam subjected to a concentrated load $P$ at the free end would have:

$$\frac{1}{\rho }=-\frac{Px}{EI}$$

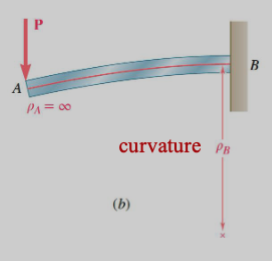
The curvature varies linearly with $x$. At the free end $A$, we have:

$$\frac{1}{{\rho }_A}=0,{\rho }_A=\infty$$

At the support $B$, we have:

$$\frac{1}{{\rho }_B}\ne 0,|p_b|=\frac{EI}{PL}$$

Overhanging Beam

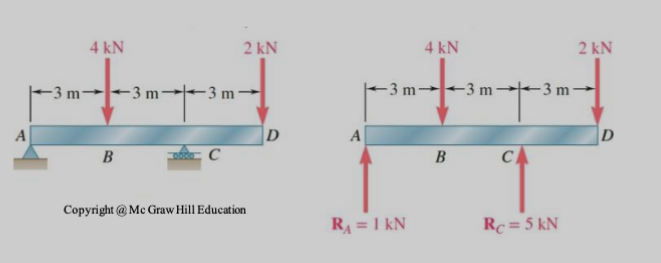
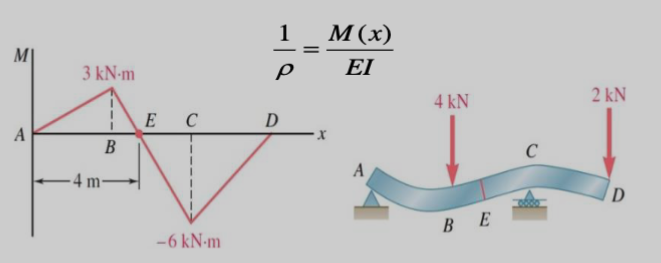
For an overhanging beam, we can examine the equation $\frac{1}{\rho }=\frac{M}{EI}$.

To analyze, we can draw the bending moment diagram.

• The curvature is zero where the bending moment is zero. Thus, the curvature is zero at the ends and at point $E$.
• If the bending moment is positive ($M+$), the deformation is concave upwards. If the bending moment is negative ($M-$), the deformation is concave down.