Beam Deflections with Superposition Method

For beam deflection due to bending, the results of many simple load cases and boundary conditions have been solved and are available. Superposition resolves the effect of combined loading on a structure by determining the effects of each load separately and adding the results algebraically.

• Deformations of beams subjected to combinations of loadings may be obtained as the linear combination of the deformations from the individual loadings.
• This is facilitated by tables of solutions for common types of loadings and support.

Furthermore, the method of superposition can be applied to determine the reactions at the supports of statically indeterminate beams. This can be done by:

• Designating one of the reactions as redundant and eliminate or modify the support
• Determine the beam deformation without the redundant support.
• Treat the redundant reaction as an unknown load which, together with the other loads, must produce deformations compatible with the original supports.

Superposition Example

For the beam and loading shown, we determine the slope and deflection at point $B$ using the superposition method.

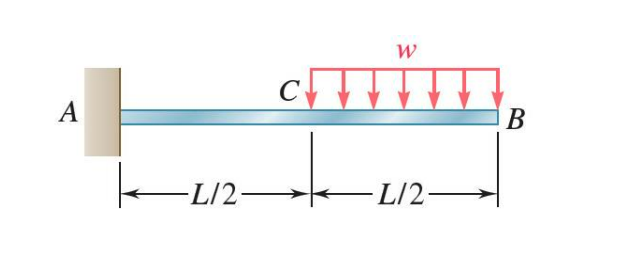
This can be done by superposing the deformations due to Loading I and Loading II as shown. The actual loading is equivalent to the superposition of these two loadings.

Loading I

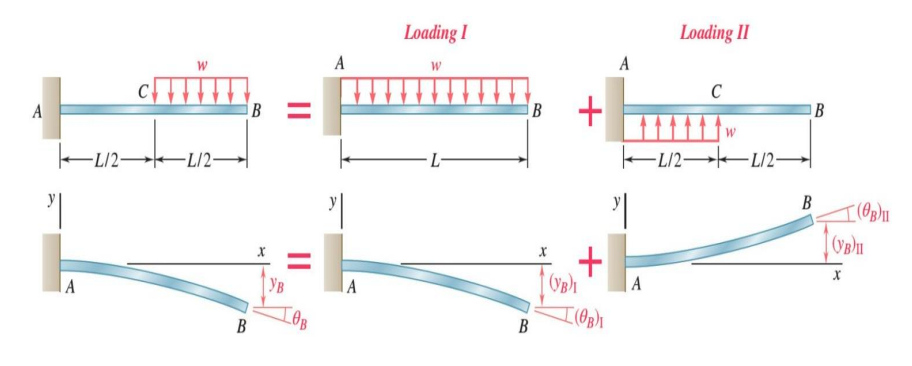
$$({\theta }_B{)}_I=-\frac{w{L}^3}{6EI},(y_B{)}_I=-\frac{w{L}^4}{8EI}$$

Loading II

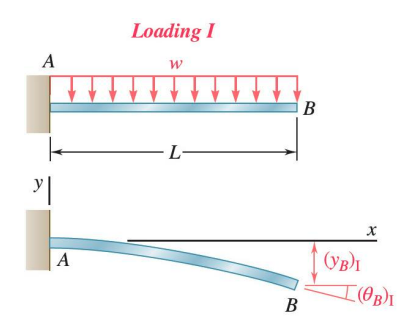
$$({\theta }_C{)}_{\text{II}}=\frac{w{L}^3}{48EI},(y_C{)}_{\text{II}}=\frac{w{L}^4}{128EI}$$

In segment $CB$, the bending moment is zero and the elastic curve is a straight line, so we ahve:

$$\begin{array}{rl}({\theta }_B{)}_{\text{II}}& =\frac{w{L}^3}{48EI}\\ (y_B{)}_{\text{II}}& =\frac{w{L}^4}{128EI}+({\theta }_C{)}_{\text{II}}\left(\frac{L}{2}\right)\\ & =\frac{w{L}^4}{128EI}+\frac{w{L}^3}{48EI}\left(\frac{L}{2}\right)\\ & =\frac{7w{L}^4}{384EI}\end{array}$$

This is shown here:

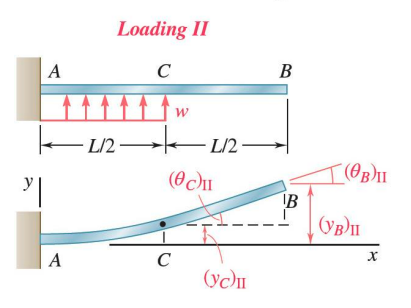
Actual Loading

The actual loading is equivalent to the superposition of the two distributed loads:

$$\begin{array}{r}{\theta }_B=({\theta }_B{)}_I+({\theta }_B{)}_{\text{II}}=-\frac{w{L}^3}{6EI}+\frac{w{L}^3}{48EI}=-\frac{7w{L}^3}{48EI}\\ y_B=(y_B{)}_I+(y_B{)}_{\text{II}}=-\frac{w{L}^4}{8EI}+\frac{7w{L}^4}{384EI}=-\frac{41w{L}^4}{384EI}\end{array}$$