Equation of Elastic Curve

How do we find the deflection of a bending beam?

Note that the slope of the beam at any point $x$ is:

$$\theta =\frac{dy}{dx}$$

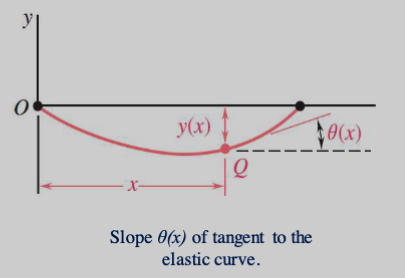
Recall that the curvature of a plane curve can be given by:

$$\frac{1}{\rho }=\frac{d^{2}y/d{x}^2}{{\left[1+{\left(\frac{dy}{dx}\right)}^2\right]}^{3/2}}\approx \frac{d^{2}y}{d{x}^2}$$

The approximation of $\frac{1}{\rho }=\frac{M}{EI}=\frac{d^{2}y}{d{x}^2}$ is based on the fact that the slope $dy/dx$ is often very small for bending. Thus, the denominator is approximately $1$.

Recall that beam deflection due to bending is given by:

$$\frac{1}{\rho }=\frac{M}{EI}$$

We can substitute and integrate:

$$\begin{array}{rl}EI\frac{1}{\rho }& =M(x)\\ EI\frac{d^{2}y}{d{x}^2}& =M(x)\\ EI\frac{dy}{dx}& =EI\theta ={\int }_0^{x}M(x)dxdx\\ EIy& ={\int }_0^{x}dx{\int }_0^{x}M(x)dx+C_{1}x+C_2\end{array}$$

Which lets us calculate the maximum deflection, $y$. The constants are determined from boundary conditions. More complex loadings require multiple integrals and application of requirement for continuity of displacement and slope.

Elastic Curve from Load Distribution

For a beam subjected to a distributed load, we have:

$$\frac{dM}{dx}=V(x),\frac{d^{2}M}{d{x}^2}=\frac{dV}{dx}=-w(x)$$

The equation for beam displacement becomes:

$$\frac{d^{2}M}{d{x}^2}=EI\frac{d^{4}y}{d{x}^4}=-w(x)$$

Integrating four times gives:

$$EIy(x)=-\int dx\int dx\int dx\int w(x)dx+\frac{1}{6}{C}_1{x}^3+\frac{1}{2}{C}_2{x}^2+C_{3}x+C_4$$

The constants are determined from boundary conditions.